dl036: graphentypen 2 – histogramme, boxplots, etc.

In unserer Reihe zu Graphentypen geht es um verschiedene Daten und welche Arten der Darstellung es für diese gibt. Im ersten Teil (dl029: graphentypen – skalen und zeiger) ging es um die kleinste Einheit: um eindimensionalen Daten. Dieses Mal wird es ein bisschen komplexer. Wir reden über Graphentypen, mit denen sich eindimensionale Verteilungen abbilden lassen. Es geht um Histogramme, Boxplots, Violinenplots und kumulierte Häufigkeiten. Welche Darstellung eignet sich für welchen Zweck? Worauf kann man bei der Auswahl des Plots achten? Und überhaupt: Womit erstellt mensch eigentlich modern aussehende Plots?

Bilder zur Folge

Histogramme

Boxplots

Violinenplot

Kumulierte Häufigkeit

Links und Quellen

• datenleben
  • www.datenleben.de
  • Social Media: Mastodon @datenleben@chaos.social und Twitter @datenleben
• Erwähnte datenleben-Folgen
  • dl029: graphentypen – skalen und zeiger
  • dl019: standarddatensätze
  • dl013: datenvisualisierung
• Die hier verwendeten Plots und der zugehörige Code
  • datenleben-blog: wie erstelle ich histogramme, boxplots und violinenplots in R?
• Datensatz
  • GitHub, Horst AM, Hill AP, Gorman KB (2020). palmerpenguins: Palmer Archipelago (Antarctica) penguin data. R package version 0.1.0.
• R und Data Science
  • https://www.tidyverse.org/
  • Hadley Wickham, Garrett Grolemund: R for Data Science (2e)

Schlagworte zur Folge

Datenvisualisierung, Graphen, Daten, Dimensionen, Histogramm, Boxplot, Violinenplot, kummulierte Häufigkeit

Intro (00:00:00)

Thema des Podcasts (00:00:18)

Helena: Willkommen zur 36. Folge beim datenleben Podcast, dem Podcast über Data Science. Wir sind Helena

Janine: und Janine

Helena: und möchten euch die Welt der Daten näher bringen. Was für Daten umgeben uns? Wie werden Daten für uns lesbar und was können wir aus ihnen lernen? Wer schon immer mehr darüber wissen wollte, ist hier richtig, denn diesen Fragen gehen wir nach.

Thema der Folge (00:00:39)

Janine: Willkommen dieses Mal zu Teil 2 unserer Reihe zu Graphentypen. In dieser Reihe geht es darum, was es für Daten gibt und welche Arten der Darstellung es für diese Daten gibt. Im ersten Teil haben wir uns eine der kleinsten Einheiten rausgesucht gehabt, nämlich die eindimensionalen Daten, und wie man sie darstellen kann, haben wir da besprochen, und auch wofür das sinnvoll sein kann, sie darzustellen, weil im Wesentlichen war es manchmal einfach nur eine Zahl. Das war Folge 29, Graphentypen – Skalen und Zeiger. Wir bleiben noch mal bei den eindimensionalen Daten in dieser Folge, aber es wird ein bisschen komplexer. Es geht nämlich um Graphentypen, mit denen sich eindimensionale Verteilungen abbilden lassen. Und dafür hat Helena sich vier Optionen rausgesucht, die sie dann gleich eben näher beschreiben wird. Das sind Boxplots, Violinen, Histogramme und kumulierte Häufigkeiten. Klingt schon mal vielversprechend. Am Ende der letzten Folge hatte sie ja schon angeteasert und sozusagen ein bisschen gespoilert, um hier jetzt noch mehr Anglizismen in den Raum zu werfen, dass Boxplots etwas sind, mit denen man sich eingehender befassen muss, um sie überhaupt zu verstehen, dann wären sie aber sehr nützlich, während Histogramme hingegen deutlich intuitiver zu verstehen seien, aber dafür auch leichter zu manipulieren. Ja, so viel dazu noch mal, ich bin schon gespannt, was da jetzt konkret hinter steckt, und gebe mir ansonsten heute vor allem Mühe, die richtigen Fragen zu stellen.

Warum ist das Thema wichtig? (00:02:17)

Helena: Ja, und warum finden wir das Thema wichtig für unseren Podcast? Nun, wie man mit Daten umgeht, ist das Kernthema von unserem Podcast, und darum beschäftigen wir uns auch, wie man sie darstellen kann.

Einspieler: Daten und ihre Dimensionen (00:02:29)

Janine: Daten und ihre Dimensionen. Manche Menschen glauben, dass die Art, wie Kaffeesatz oder Tee sich in einer leeren Tasse auf dem Boden absetzen, einen Blick in die Zukunft ermöglicht. Egal, was dabei herauskommt, das Prophezeite klingt für die meisten Menschen heutzutage nicht sehr plausibel, und schließlich gibt es ja die Wissenschaft, die ist schon viel weiter. Es gibt so viele Daten über eigentlich alles, da können wir doch fast alle Ereignisse in unserem Realitätssystem vorhersagen, sogar das Wetter oder wie Kometen durch das All fliegen. Aber trotzdem wissen wir noch gar nicht alles, obwohl wir es ja vielleicht könnten, es sind so viele Daten, da müsste doch eigentlich sich alles mit erklären lassen, oder? Allerdings machen viele Daten es nicht auch manchmal eher schwieriger zu verstehen, was sie einem aufzeigen könnten? Wenn wir auf die Masse an Daten gucken, die wir heutzutage sammeln, kann einem der Gedanke kommen, dass das nicht viel präziser sein kann, als wenn jemand allen Kaffeesatz oder Tee auf einen großen Haufen gekippt hat und ein Schild davor stellt, auf dem steht, ich habe die Welt restlos untersucht und kann alles erklären. Also, theoretisch zumindest, denn die Antworten müssen ja da drinnen in diesem Haufen stecken. Nur irgendwer muss sie irgendwie da rausholen. Für diese Menschen gibt es sogar einen Namen, die das machen, Data Scientists. Sie müssen an diesen großen Haufen gehen und die Daten rausfiltern, die relevant sind. Dabei ist es oft sogar hilfreich, nicht nur weniger verschiedene Daten zu untersuchen, sondern auch weniger komplexe Daten auszuwählen. Die Frage von Data Scientists ist nicht, wie kann ich möglichst viel auf einmal erklären, sondern: Was ist der Kern meiner Frage und welche Daten brauche ich dafür wirklich? Wenn ich wissen möchte, wie viel Zeit ich am Handy verbringe pro Tag, dann nehme ich eine Messung vor. Sagen wir, immer zur gleichen Zeit an jedem Tag über eine Reihe von Tagen. Messzeitpunkt 23 Uhr 59, 3 Stunden an diesem Tag, 4 Stunden an jenem Tag etc. Soweit erst einmal einfach, aber gleichzeitig bietet dieser Messzeitpunkt viel mehr Daten. Wochentag, Arbeitstag oder Wochenende, das wären theoretisch Faktoren, die mein Verhalten beeinflussen. Dann müsste ich aber viel mehr und viel genauer erfassen. Aber brauche ich das? Eigentlich möchte ich nur wissen, was in etwa meine Handynutzung pro Tag ist. Für eine grobe Schätzung meines Verhaltens würde mir das reichen. Ich kürze also alle überflüssigen Dimensionen raus und konzentriere mich auf genau einen Wert über einen bestimmten Zeitraum. Damit kann ich eine eindimensionale Verteilung erstellen. Die konkrete Frage lautet: Wie viele Stunden bin ich pro Tag am Handy über 36 Tage hinweg? Das heißt, ich werde 36 Messergebnisse erfassen und analysieren. Daraus kann ich dann zum einen die durchschnittliche Nutzungsdauer ausrechnen, also die erfasste Stundenzahl insgesamt durch 36 geteilt, zum anderen aber auch die mittlere Nutzungsdauer. Das wäre der Median, 50% der Werte liegen über und 50% der Werte liegen unter dem Median. Diese beiden Betrachtungen können mir dabei helfen, ein gutes Gefühl dafür zu erhalten, wie viel Zeit ich am Handy verbringe und damit kann ich mir überlegen, ob das Ergebnis okay für mich ist oder ob ich etwas optimieren möchte. Wenn es okay ist, habe ich einen guten Eindruck und eine Entscheidung gewonnen, es kann so bleiben, wie es ist. Wenn ich etwas ändern möchte, weiß ich aber auch, dass es sich lohnen könnte, mir die Daten genauer anzusehen und vielleicht weitere Dimensionen zu betrachten, meine Fragestellung zu konkretisieren und damit vielleicht auf den Grund zu kommen, warum an welchen Tagen ich wie viel das Handy nutze und wie ich das eventuell anders machen kann.

Worum geht es, was sind die Ausgangspunkte? (00:06:29)

Helena: Ja, diesmal geht es um Diagramme für eindimensional verteilte Daten, also das heißt man hat nicht nur einen Datenpunkt zu einem Zeitpunkt, sondern ganz viele davon und wie man das dann darstellen kann, um ein Gefühl dafür zu bekommen, das ist das heutige Thema. Beim letzten Mal ging es ja um einen konkreten Datenpunkt zu einem bestimmten Zeitpunkt, wenn man drauf guckt und jetzt geht es darum, wenn man ganz viele davon hintereinander aufgeschrieben hat, was man dann damit tun kann, also um die Verteilung der Daten.

Janine: Wir hatten ja beim letzten Mal alltägliche Beispiele mit reingebracht, das war zum Beispiel jetzt der Wasserkocher, wo drauf angezeigt wird, wie viel Wasser drin ist oder die Küchenwaage, die in dem Moment des Abwiegens anzeigt, wie viel etwas wiegt, das ich gerade benutzen möchte, oder eben die Luftpumpe, die anzeigen kann, wie groß der Luftdruck im Reifen schon ist, beziehungsweise wie niedrig. Gibt es auch so prägnante Beispiele für eindimensionale Verteilung?

Helena: Ja, also eine Möglichkeit wäre, du kannst jedes Mal mitschreiben, wie viel Wasser du im Wasserkocher hast und weißt dann immer, ja, wie viel benutzt du denn tendenziell. Oder auch etwas, was mir mein Handy zum Beispiel einmal die Woche dann für die vergangene Woche mitteilt ist, wie viele Stunden am Tag benutze ich das Handy und das wird dadurch eine Verteilung, dass ich ganz viele Tage habe, die ich dann vergleichen kann. Oder auch, wie groß sind Menschen, ich habe irgendwie einen Raum voller Menschen und dann sehe ich, manche sind größer, manchmal kleiner und dann ist eben die Größe eben diese eindimensionale Verteilung, gerade wenn mir egal ist, welche Menschen genau jetzt wie groß sind, sondern es nur darauf ankommt, ja, dass die Größe unterschiedlich verteilt ist. Und ein anderes Beispiel wäre zum Beispiel, wie viel Energie ich pro Tag verbrauche. Dafür gibt es ja auch so Anzeigen bei mir in der Wohnung für Gas und Strom und da kann ich dann ablesen, wie der tägliche Energieverbrauch war, beziehungsweise kann ich zu dem Zeitpunkt ablesen, wie der aktuelle Stand ist vom Zähler und daraus dann wieder den Energieverbrauch pro Tag zurückrechnen.

Janine: Klingt auf jeden Fall direkt schon mal praktisch anwendbar. Ich dachte mir, vielleicht kann es helfen, wenn ich versuche, noch mal einen kleinen Überblick über das zu geben, was wir so in der letzten Folge angesprochen haben. Ich habe vor allem aus der Folge mitgenommen, dass eindimensionale Daten mich eben über einen aktuellen Zustand informieren können. Im Alltag ist es halt meist eine einzige Anzeige, aber diese Daten sind eben nicht gleich zu sitzen mit Informationen, die ich daraus ablese. Das Thema hatten wir beim letzten Mal auch, den Unterschied zwischen Daten und Informationen, weil Informationen sind eigentlich interpretierte Daten. Ob 0,7 Liter für zwei Tassen reicht, muss sich eben selbst entscheiden. Deswegen hatten wir gesagt, man muss also auch den Kontext kennen, um die Daten benutzen zu können. Beim Zeigerdiagramm gab es zum Beispiel, das hatte Helena ganz gut beschrieben, die Möglichkeit, den Kontext gleich mitzuliefern, damit nämlich niemand auswendig wissen muss, wann der Reifen gut befüllt ist, zeigt das Diagramm selbst schon einen Messbereich an von bis, in dem der Zeiger idealerweise liegen sollte, d.h. wenn ich den Luftdruck meines Reifens messe, kann ich überprüfen, wann er in diesem Bereich ist, während ich Luft aufpumpe. Das ist auch der letzte wichtige Punkt, den ich aus der Folge mitgenommen habe, denn für welche Darstellung man sich entscheidet, ist auch immer kontextabhängig, d.h. ich kann über die Darstellung auch Kontext mitliefern und damit bereits aus den Daten Informationen machen. Das wird dann vielleicht interessant, wenn wir darüber reden, je nachdem, wie ausführlich das wird, inwiefern man mit Diagrammen Darstellungen von Daten manipulieren kann. Kommen wir dann mal zur großen Frage dieser Folge. Was habe ich denn bei eindimensionalen Verteilungen für Optionen zur Darstellung und langfristig schon mal die Frage mit drangehangen, warum ausgerechnet die?

Was sind Histogramme? (00:10:30)

Helena: Ja, da hast du ja am Anfang schon ein paar genannt und anfangen würde ich mit den Histogrammen. Histogramme sind Balkendiagramme, die die Häufigkeit darstellen. Ein Beispiel, weil wir das alle aus unserem Alltag kennen, ist die Darstellung von Wahlergebnissen und zwar werden die oft als Balken dargestellt. Die Daten selber liegen quasi in Form von Stimmzetteln vor und in diesem Stimmzettel hat man dann eben eine Liste von Parteien und eine Partei, die angekreuzt wurde, ist dann eben ein Datenpunkt und wenn man ganz viele Stimmzettel hat, hat man eine Verteilung von verschiedenen Stimmzetteln. Es ist völlig egal, in welcher Reihenfolge die Stimmzettel gezählt werden, weil es nur am Ende auf die Häufigkeit der Stimmverteilung angeht und so ein Histogramm zeigt dann eben an, wie häufig etwas gewählt wurde. Im Falle von Wahlen wird meistens das Ganze dann noch in den relativen Stimmanteil umgerechnet also man teilt es noch durch die Gesamtzahl aller Stimmen, um eine Prozentzahl anzuzeigen statt der Gesamtstimmenanzahl, aber im Grunde genommen ist es eben das Gleiche. So, die eine Dimension, die dargestellt wird, besteht eben aus verschiedenen möglichen Ausprägungen in Form von Parteien, die man angekreuzt haben kann und dargestellt wird es dann eben in Form von Balken, die dann eine Prozentzahl anzeigen bzw. man könnte auch die Gesamtstimmenzahl dran schreiben.

Janine: Nur, dass die Balken dann wahrscheinlich extrem viel höher wären.

Helena: Naja... es ist alles eine Darstellung...

Janine: Man kann die Skala, okay.

Helena: Also die Höhe kann man jetzt skalieren.

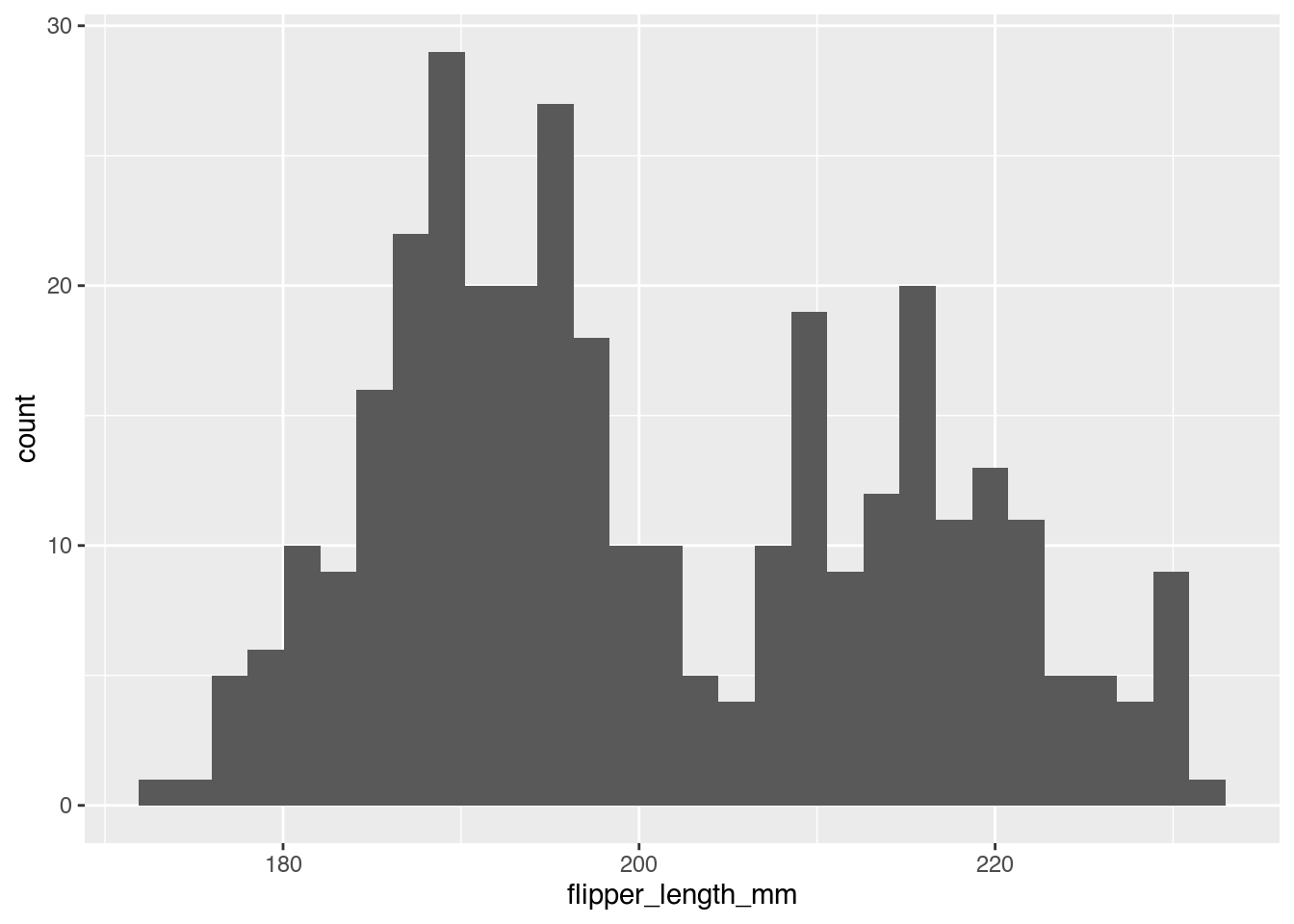
Helena: Genau, und in diesem Fall ist in dieser einen Dimension... sind die verschiedenen Parteien, also letztlich sind das Kategorien von Stimmen und meistens gibt es ja dann noch sonstige, wo man halt alle anderen so zusammenfasst, das heißt auch da passieren noch andere Zusammenfassungen, aber da sind die Kategorien schon vorgegeben für die Balken, die man darstellen möchte. Eine andere Möglichkeit, Histogramme darzustellen, ist, wenn man jetzt nicht irgendwie Kategorien hat, die eine bestimmte Häufigkeit haben, sondern z.B. die Größenverteilung von Menschen oder z.B. die Flossenlänge von Pinguinen. Und dann hat man irgendwie ein paar hundert Pinguine und misst einmal, wie lang sind deren Flossen und auch da kommt es einem jetzt nicht darauf an, welcher genauer Pinguin man da ausgemessen hat und dann kann man dann für jede Flossenlänge so einen Balken zeichnen und so eine Flossenlänge ist aber kontinuierlich, das heißt, das kann irgendwie 19 cm lang sein, das kann aber auch 22 cm lang sein und alle Werte dazwischen sind auch möglich, das heißt, um so einen Balken zu zeichnen, muss man die zusammenfassen, also z.B. 1 cm Schritte oder auch 2 cm Schritte oder wenn man so ein Histogramm zeichnet, kann man auch sagen, ja, ich möchte am Ende 30 Balken haben, dann kann man ausrechnen, ja, wie groß müssen die denn sein, wenn alle Balken gleich dick sein sollen und da hat man dann eben die Auswahl zwischen verschiedenen Balkenbreiten und entsprechend kann man dann auch ein bisschen Einfluss darauf nehmen, wenn man möchte, wie genau am Ende das Ergebnis aussieht, das ist der Teil, den ich mit manipulieren meine, dass man dadurch, dass man die Position der Balken in diesem Fall selber bestimmen kann, könnte man da auch einfach ein bestimmtes Ergebnis mit erzeugen, falls die Daten das überhaupt hergeben, ich meine, auch da müssen dann immer noch die Daten dazu passen, aber dann könnten komplett reale Daten immer noch eine komische Interpretation erlauben, das ist halt so das eine Risiko hier. Genau. Ja, zu den Pinguinen, das haben wir nämlich genau auch als Beispiel, das ihr auch in den Schaunals euch angucken könnt, und die Flossenlängen von Pinguinen haben wir einmal dargestellt. Janine, magst du einmal beschreiben, was du siehst?

Janine: Ja, ich gebe mir die größte Mühe. Vor mir ist ein monochromes Histogramm, also die Balken sind grau und der Hintergrund ist auch leicht gräulich, es hat auf der x-Achse, das ist die, die horizontal verläuft, da steht Flipper-Length, also die Flossenlänge der Pinguine, und auf der y-Achse, die eben senkrecht nach oben geht, da ist die Anzahl angegeben, Count, von 0 bis 30, und die Flossenlänge ist irgendwie in drei Schritten angegeben, 180, 200 und 220, und ja, da drin sind relativ schmale Balken, die aber nicht, wie man das jetzt bei den Wahlergebnissen kennt, separiert voneinander nebeneinander stehen, sondern da gibt es keine Lücken zwischen den einzelnen Balken. Deswegen entsteht eigentlich ein Gebilde mit einer durchgehenden Fläche, das nach oben hin sozusagen von einzelnen Balken, so wie... so ein bisschen treppenstufenmäßig kann man sich das vorstellen, abgeschlossen wird, und was mir vor allem als erstes auffällt, ist, dass es eigentlich zwei Bereiche gibt, die auffallen, nämlich es fängt mit sehr kleinen Balken an, geht dann recht schnell bis zu mittleren Balkenhöhen, wird einmal ganz groß, bis fast zur 30 hoch, fällt einmal ab, hat nochmal einen Peak, bis fast zur 30 hoch, und fällt dann weit unter 5, relativ steil runter, um danach nochmal anzusteigen und nochmal hochzugehen und dann wieder runter, sozusagen, und am Ende ist noch einmal ein kleinerer Peak nach oben. Das heißt, von der Form her sind es also zwei Hügel, die da entstanden sind, eigentlich, wenn man das jetzt mal so abstrakter betrachten würde, und das finde ich schon ganz spannend.

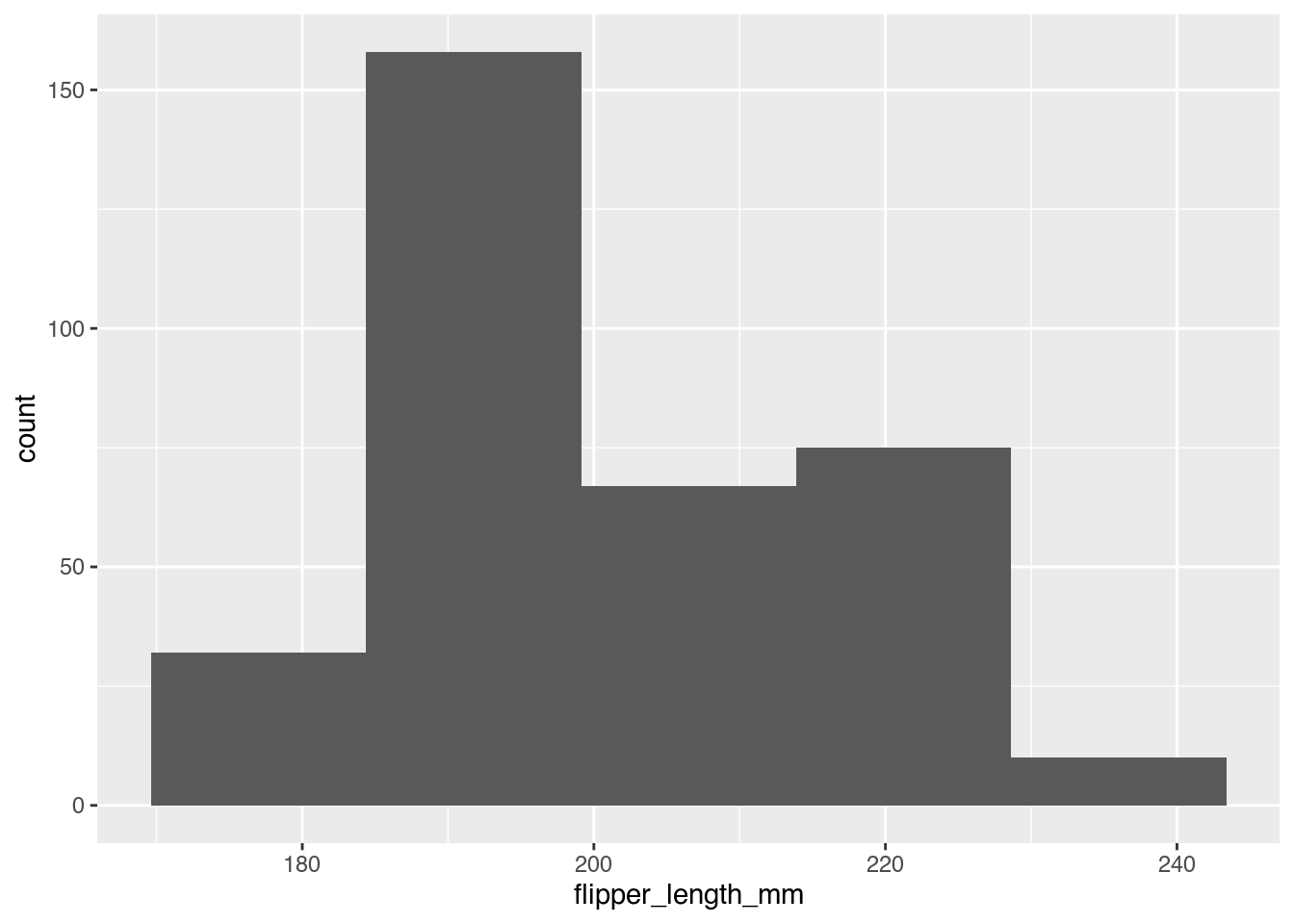
Helena: Genau, und das war jetzt das Beispiel, wo 30 Balken gezeichnet wurden und dieselben Daten, wenn man die jetzt nur in 5 Balken darstellt, sehen ja ein bisschen anders aus. Das ist dann das nächste Bild.

Janine: Genau, also die Beschriftung an den Achsen ist annähernd die gleiche. Hier gehen die 5 Balken auch ineinander über, sie sind relativ breit, und der erste Balken geht bis zur 40 oder so, sage ich mal, der zweite Balken geht dann sofort nach oben, bis über 150, der dritte fällt irgendwo auf die 70 runter, der vierte Balken ist knapp da drüber, und der fünfte Balken ist ziemlich flach, wenn überhaupt, 10. Also die Form, die hier entsteht, ist irgendwie so eine Stufe, dann eine riesige Stufe, ein bisschen wieder nach unten, relativ gerade, und hinten nochmal steil nach unten.

Helena: Ja, und die Zahlen sind ja auch deutlich höher, weil jetzt natürlich mehr Pinguine zusammengefasst wurden pro Balken, weil die sind ja jetzt auch deutlich breiter.

Janine: Ja.

Helena: Und vom Gefühl her, was du gerade mit den zwei Hügeln beschrieben hast, bei dem ersten Histogramm, ist ja jetzt gar nicht mehr so deutlich sichtbar im zweiten.

Janine: Nee, da ist nur nochmal eine kleine Kante nach oben,

Helena: Ja.

Janine: aber die fällt jetzt irgendwie nicht weiter auf... ja.

Helena: Genau, und das ist ungefähr das, was ich meinte, was man mit der Wahl der zusammengefassten Daten kann man halt auch ein bisschen an der Darstellung beeinflussen und potenziell dann auch ein gewünschtes Ergebnis erzeugen. Was man dadurch verhindern kann, dass man einfach automatische Tools benutzt und dann guckt, ja, kann ich daraus sinnvolle Sachen lesen. Eine Sache, die man hier auf jeden Fall auch vermeiden sollte, ist, wenn man jetzt, keine Ahnung, nur 20 Datenpunkte hätte, dann auch 20 Balken zu zeichnen, die dann alle gleich groß sind und die nicht zusammenzufassen, weil dann bringt einem dieses Histogramm auch genau gar nichts, wenn alle Balken bei 1 sind und dann ab und zu mal stattfinden. Das ist komplett sinnfrei, das kann man dann besser lassen.

Janine: Das heißt, um mal dazwischen zu fragen, Histogramme eignen sich vor allem gut auch, um Gruppen darzustellen, also wie bei der Wahl eben zum Beispiel.

Helena: Ja, wenn man entweder schon klare Kategorien hat wie bei der Wahl, also wenn die Werte ja im Prinzip ausgezählte Stimmen sind, wie oft kommt eine Kategorie vor, dann ist das ziemlich genau das, was man haben will. Ja, und eine Sache, die du ja auch schon erwähnt hast, ja, das Balkendiagramm hat eine x-Achse und eine y-Achse und das... sind das nicht Zwei Dimensionen?

Janine: Ja, stimmt.

Helena: Ja, also die grafische Darstellung, das Histogramm selber ist zweidimensional, weil nur eine Dimension wäre ja nur eine Linie und in einer Linie kann man nicht so richtig gut was darstellen. Deswegen ist die Darstellung zweidimensional, aber das was... die Häufigkeit ist ja etwas, was komplett aus den Daten ausgerechnet wird. Das heißt, die zweite Achse, die man benutzt, um es darzustellen, wird komplett ohne weitere Informationen aus der ersten Achse ausgerechnet, aus der eindimensionalen Verteilung und das gilt auch für alle anderen Plottypen, die heute noch kommen, dass das, was man dann auf der y-Achse darstellt, ausgerechnete Werte sind, die auf der Verteilung basieren. So wird dann eben die zweite Dimension in der Darstellung eingeführt, während man trotzdem nur eine eindimensionale Verteilung darstellen möchte.

Janine: Und das gilt dann auch zum Beispiel für Zeitpunkte? Also du hattest ja das Beispiel mit dem Handy gebracht. Wenn ich jetzt sage, wie viele Stunden pro Tag bin ich am Handy gewesen? So, dann habe ich ja auf der x-Achse könnte ich dann angeben, meinetwegen die letzten sieben Tage und auf der y-Achse die Stunden als Einheit. Kann ich das da auf die gleiche Art und Weise kategorisieren, wie du es eben gemacht hast oder sind es dann doch zwei Dimensionen in dem Fall?

Helena: Doch, in dem Fall sind das schon zwei Dimensionen, weil der Tag, an dem das ist, eine Rolle spielt. Wenn du jetzt nur aufschreiben würdest, wie lange du an einem Tag am Handy warst und dann am Ende es aber keine Rolle mehr spielt, an welchem Tag das war, dann hast du nur noch eine Dimension. Aber sobald der genaue Tag eine Rolle spielt, hast du auch noch die Dimension Zeit, die eine Rolle spielt mit drin.

Janine: Mhm.

Helena: Und ich meine, das ist dann immer noch ein Balkendiagramm und Histogramme sind ja auch Balkendiagramme, aber ja, das, was sie darstellen, ist schon inhärent dann zweidimensional, wenn sie das auf Wochentage beziehen.

Janine: Und in dem Beispiel mit den Menschen ist es dann deswegen nicht zweidimensional, wenn ich auf der x-Achse meinetwegen die Größe eines Menschen angebe und auf der y-Achse, wie oft diese Größe in meiner Gruppe vorkommt, die ich gemessen habe, dann ist die Messung, die ich mache, die Größe und die Anzahl wieder der abgeleitete Wert, weswegen es wieder eindimensional ist.

Helena: Genau, die zugrundlegende Verteilung ist eindimensional, ja.

Janine: Okay. Ja, ich glaube, damit kann ich was anfangen. Das hätte ich letztens gebraucht, als ich mal das Thema angesprochen habe, aber ich kann das ja jetzt einfach weiterreichen.

Helena: Genau, ich hoffe, das hilft auch generell. Ich möchte noch mal auf die Hügel zurückkommen. Du hast ja gesagt, man sieht im Prinzip zwei Hügel in der Flossenlängenverteilung bei den Pinguinen. Und wenn ich jetzt so ein Histogramm hier angucke, wo dann so zwei so Hügel sind, dann ist so meine erste Idee, ja, vielleicht gibt es auch einfach zwei Kategorien von Pinguinen und die einen sind halt größer als die anderen. Und vielleicht sind das zwei verschiedene Pinguinarten, die zusammengepackt wurden in eine Grafik.

Janine: Lass mich raten, du kommst auf diese Idee mit den zwei Gruppen, ich glaube, ich wäre es im ersten Moment nicht, weil du diese Sache mit diesem Gauß und der Normalverteilung und der Glockenkurve im Kopf hast, oder?

Helena: Ja, genau, weil so eine natürliche Größe ist halt immer, also Menschen sind ja auch ungefähr ähnlich groß. Es gibt natürlich Ausreißer, aber im Schnitt gibt es da auch eine bestimmte Verteilungsform. Manche Leute sind größer, manche kleiner, aber wenn man alle zusammenzählt, hat man halt nur so eine bestimmte Kurvenform. Das ist ja dann die Gauß'sche Glockenkurve. Beziehungsweise ist das eines der Modelle, die man da gut ranlegen kann und das kommt auch in der Physik sehr oft vor, deswegen bin ich da auch sehr mit vertraut. Und wenn man dann zwei solche Glockenkurven hat, die verschiedene Ursachen haben und in einer Grafik zeichnet, dann hat ja verschiedene Ursachen und deswegen, wenn ich dann zwei so glockenartige Dinge oder zwei Hügel sehe in so einem Histogramm, denke ich, ja, das sind doch wahrscheinlich zwei verschiedene Dinge zusammengemischt, zum Beispiel zwei Arten Pinguine. Das wäre jetzt so bei der Grafik das, was ich zuerst denken würde, wenn ich da drauf gucke.

Janine: Lass mich raten, du hast recht.

Helena: Äh, nicht ganz. Also die Daten, wir benutzen jetzt, das wisst ihr vielleicht aus unserer Standarddatensitzefolge, den Datensatz über die Pinguine, den man sich auch einfach runterladen kann und wenn man dann die Pinguin-Spezies noch mitplottet, also wenn man ein Histogramm pro Spezies erstellt, dann sehe ich, dass das sogar drei Spezies sind.

Janine: Okay.

Helena: Und zwei davon sind so nah aneinander von der Größenverteilung, dass sie halt mehr oder weniger wie ein gemeinsamer Hügel aussehen. Die dritte Spezies, die Gentoo-Pinguine, sind halt deutlich größer als die Adelie- und die Zügel-Pinguine.

Janine: Ja.

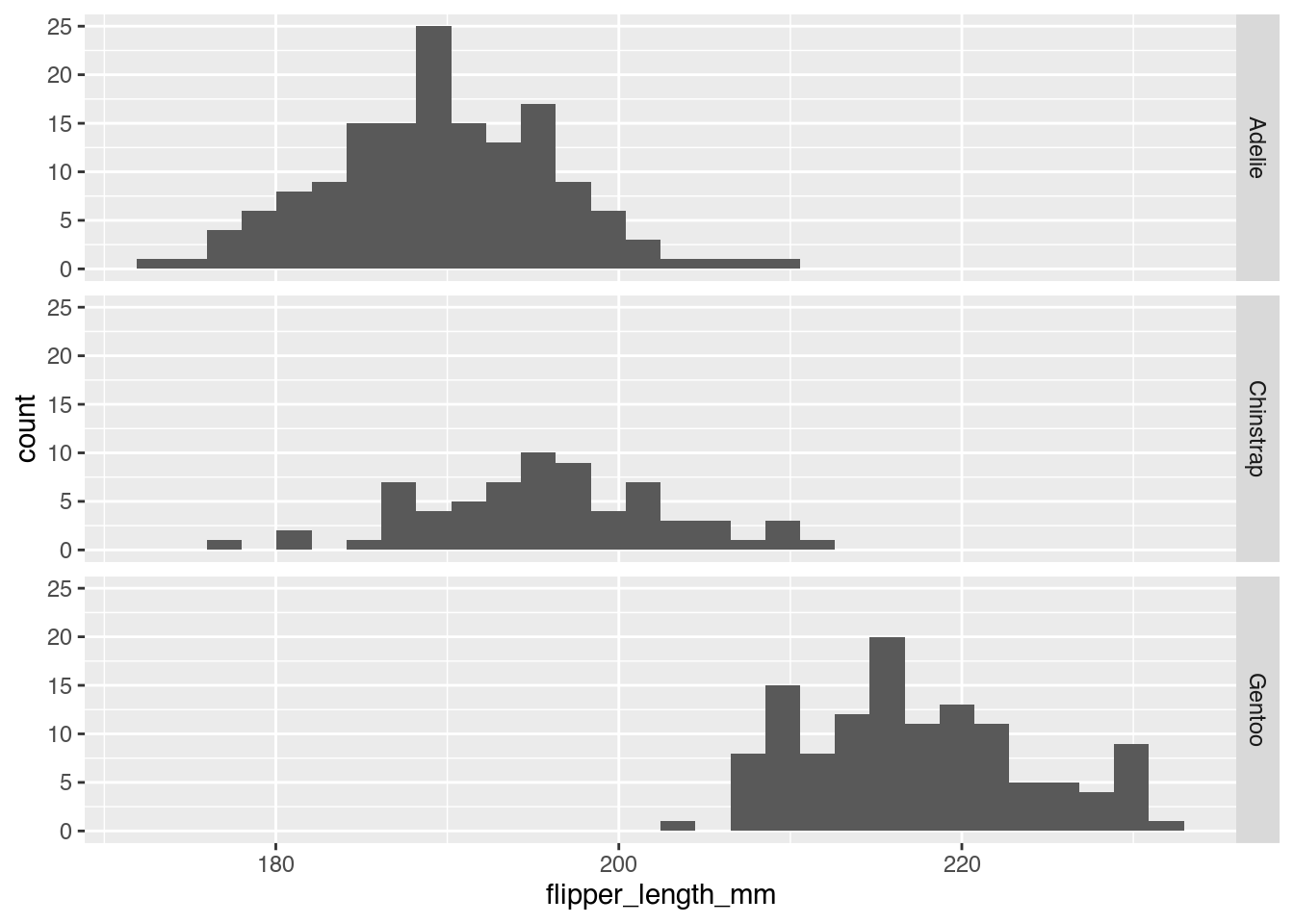
Helena: Das ist dann in der nächsten Grafik dargestellt, nämlich drei Histogramme untereinander, weil das eine Möglichkeit ist, wie wenn man jetzt innerhalb des Histogramms verschiedene Kategorien auseinanderhalten möchte, kann man die zum Beispiel so untereinanderplotten, wo dann die x- und y-Achsen genau gleich sind, sodass man auch wirklich vergleichen kann, wie häufig die vorkommen.

Janine: Ja, ich habe es mir hier gerade mal aufgemacht. Ja, also es ist, wie du gerade sagst, das sind die drei einzelnen Histogramme in dem Plot, sodass sie sich die x-Achse teilen und die y-Achse gibt es quasi dreimal, nämlich dreimal übereinander auf der gegenüberliegenden Seite der y-Achse – ist das dann y-b? – da stehen die Gruppennamen, also der Pinguin-Art. Was da halt zu sehen ist, ist jetzt, dass, ja, die erste Gruppe ganz oben, die sitzt relativ weit links, also was die Flossenlänge angeht, fängt die als erstes an und hat dann tatsächlich, joar jetzt nicht unbedingt die perfekte Glockenform, aber es geht schon arg in die Richtung. Bei der zweiten Gruppe das Gleiche, nur die ist deutlich flacher, aber man sieht, dass sie ihren höchsten Punkt hat an einer Stelle, wo die Gruppe darüber auch in etwa genauso hoch ist. Und da ist wahrscheinlich die Überlappung passiert, weswegen wir nur zwei Hügel und nicht drei im ersten Histogramm gesehen haben.

Helena: Mhm.

Janine: Ja, und die dritte Gruppe ganz unten, die fängt dann halt ziemlich weit hinten auf der x-Achse an und das ist dann eben der zweite Hügel. Man kann sich das ganz gut vorstellen, wenn man das jetzt so wieder ineinander schieben würde, entsteht eigentlich das, was man oben schon gesehen hat.

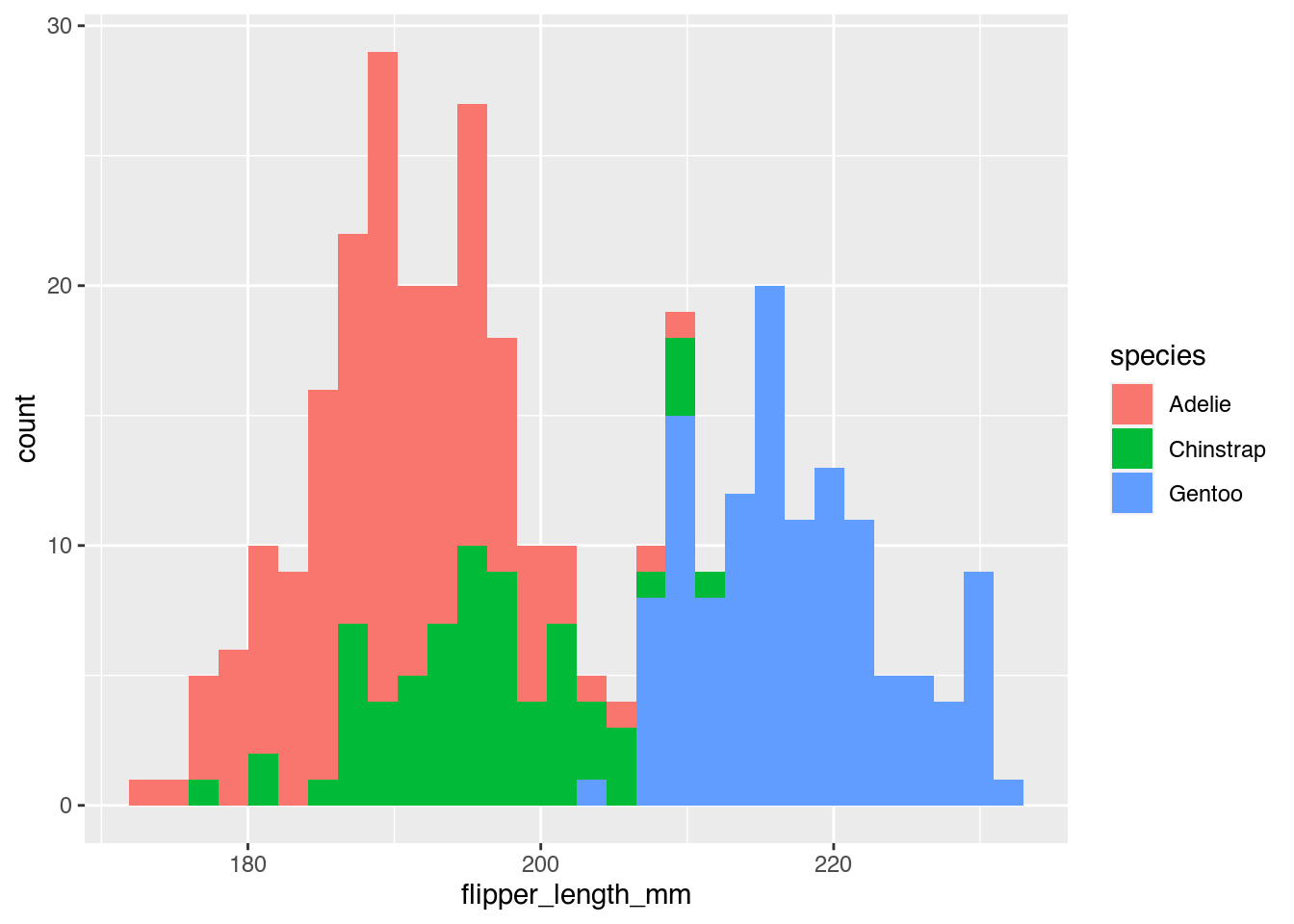
Helena: Genau. Ich glaube, aber eine Methode, die etwas häufiger ist, die ich persönlich allerdings etwas weniger deutlich verständlich finde, ist eben nicht diese drei Histogramme untereinander zu ploten, sondern einfach wie bei unserem ersten Histogramm die Grafik zu nehmen und dann einfach den Spezies verschiedene Farben zu geben. Dann kriegt man auch so ein bisschen das Gefühl dafür, wie oft die so sind, aber ich finde, es ist deutlich schwieriger, auseinanderzuhalten. Also das ist dann unser nächstes Beispiel, wo die dann farblich dargestellt sind. Aber dann ist jetzt hier zum Beispiel von den Adelie-Pinguinen, von dem größten Pinguin, ist der Punkt dann halt ganz weit oben auf dem Histogramm gezeichnet, weil darunter die anderen beiden Pinguinarten eingezeichnet sind. Und dann ist das nicht mehr so eine schöne Form, wie die zusammenhängen und das finde ich, wenn man jetzt die Häufigkeiten vergleichen will, schwerer zu lesen.

Janine: Ja, definitiv. Es ist, ja wie du sagst, der mit der größten Flosse von den Adelie-Pinguinen, der tanzt halt mit seinem einen Datenpunkt irgendwo bei der 20 auf der y-Achse rum und hat keinen Anschluss mehr zu der restlichen Gruppe, die ist irgendwo weiter unten, weil der eben auf so einen Hügel mit hochgenommen wurde sozusagen.

Helena: Ja. Aber ich glaube, so eine farbliche Darstellung ist trotzdem relativ üblich, deswegen sollte man sie erwähnen. Aber ich mag eben diese untereinander geplotteten Sachen lieber, weil da auch deutlicher wird, dass jetzt die Zügel-Pinguine auch einfach deutlich weniger in dem Datensatz vorhanden sind. Ach so, das sind ja nicht relative Häufigkeiten, wie oft ist diese Pinguin-Art vorgekommen, sondern die Gesamthäufigkeit in der verschlossenen Größen und dadurch, dass das so viel flacher ist, aber nicht wirklich breiter als die anderen, sind das auch einfach weniger Pinguine.

Janine: Ja.

Helena: Und die miteinander vergleichen zu können, muss man halt berücksichtigen, dass es weniger Pinguine sind. Eine Sache, weil du das Thema Glockenkurve schon angesprochen hast, was man sehr schön aus Histogrammen eben machen kann, ist dann so eine Glockenkurve als Modell dadran anpassen, weil man die berechneten Histogrammdaten nehmen kann, um dann wieder halt eine Fit-Funktion zu machen und dann kriegt man die Parameter von so einer Glockenkurve zu der Verteilung. Ich meine, bei der Gauß'schen-Glockenkurve sind es ja auch einfach Mittelwert und Standardabweichung, da braucht man theoretisch kein Histogramm für, um das auszurechnen, aber da könnte man anhand des Histogramms sehen, ob dieses Modell irgendwie Sinn macht oder ob die doch sehr stark abweichen. Dafür sind Histogramme eben auch gut geeignet, um ja, so Modelle daran anzuwenden, wenn sie Sinn machen.

Janine: Grob zusammengefasst, Histogramme sind eine Form des Balkendiagramms und sie eignen sich vor allem gut, um Gruppen darzustellen und die Häufigkeit von etwas in diesen Gruppen oder in Kategorien, die man erzeugt hat. Und es ist wichtig darauf zu achten, wie man Daten zusammenfasst, also wie... welche Gruppen man bildet sozusagen, weil das Einfluss auf die Darstellung und damit auch auf das Verständnis des Histogramms dann hat.

Helena: Genau.

Janine: Okay.

Helena: Dann kommen wir zum nächsten Thema.

Was sind Boxplots? (00:28:53)

Janine: Ja, ich habe ja schon gesagt, du meintest, diese Boxplots seien etwas, womit man sich erst mal länger beschäftigen muss, was macht die denn genau aus?

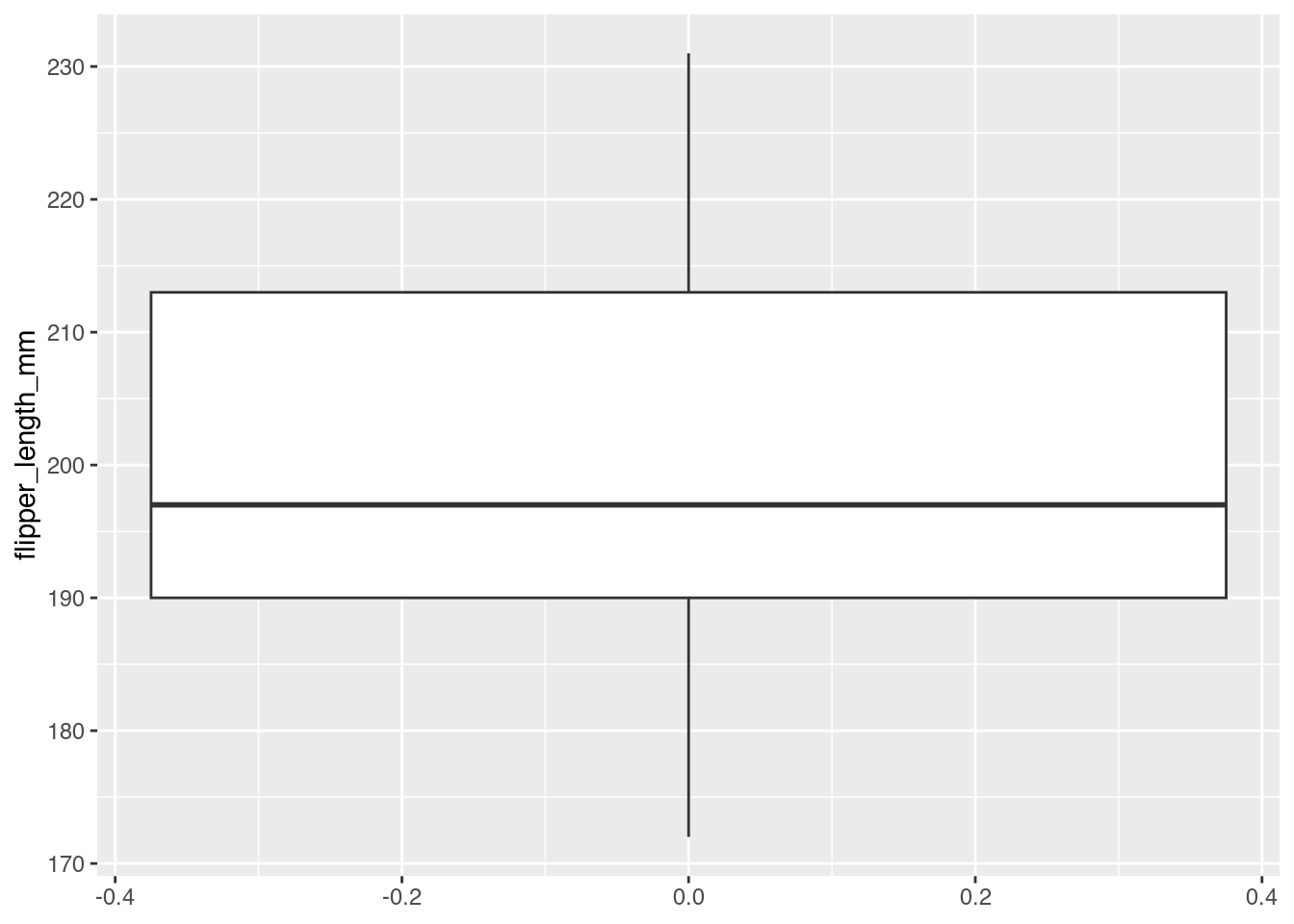
Helena: Ja, genau. Was macht ein Boxplot aus? Erstmal ist es einfach eine Box, die dargestellt wird, so eine rechteckige Box und in der ist meistens da noch eine Linie eingezeichnet, die ist irgendwo in dieser Box drin und dann gibt es oben und unten noch so Striche, senkrechte Striche, die aus den Boxen rauskommen. Und die haben eine ganz eindeutig definierte Bedeutung und zwar, die Box fängt bei 25% der Daten an und das ist dann die untere Kante von der Box und die obere Kante von der Box ist bei 75% der Daten. Das heißt, die Hälfte der Daten ist innerhalb dieser Box und die Linie in der Box selber stellt den mittleren Datenpunkt dar, also die Hälfte der Daten ist dann kleiner als diese Linie und die andere Hälfte der Daten ist größer als diese Linie, das ist auch der sogenannte Median, der mittlere Wert. Nicht zu verwechseln mit dem Mittelwert, den man anders berechnet. Der Mittelwert und der Median können ähnlich sein, müssen aber nicht auf der gleichen Stelle sein, weil wenn so eine Verteilung sehr verzerrt ist und eben keine saubere Glockenkurve, dann sind Median und Mittelwert sehr weit auseinander und je weiter die auseinander sind, desto weiter sind die halt von so einer Glockenkurve entfernt und der Boxplot zeigt aber nur den Median an. Ja, dann gibt es noch die Linie unten und die Linie oben und die untere Linie fängt quasi bei dem untersten Wert an und geht dann bis zur Box, das heißt, die stellt das untere Viertel der Daten dar und die obere Linie entsprechend das obere Viertel der Daten. Das heißt, im Grunde genommen berechnet man aus den Werten, die man hat in der Verteilung fünf Zahlen, also einmal den Median, den unteren Wert, den oberen Wert, also Minimum und Maximum und dann eben noch 25% und 75%, das sind dann sogenannte Quantile. Also diese fünf Zahlen spielen dann eben eine Rolle und die werden einfach dargestellt grafisch. Manchmal kann es noch sein, wenn man sehr viele Daten hat, aber nur einzelne davon liegen, sehr weit draußen, dass man dann noch einzelne Punkte oberhalb und unterhalb der Linie macht. Das sollen dann Ausreißer darstellen, die stellen dann nur einen kleinen Prozentsatz der Gesamtdaten dar. Ja, und das Ganze kann man dann eben auch auf die Pinguine anwenden und das, was wir im allerersten Histogramm dargestellt haben, haben wir jetzt auch in dem ersten Boxplot dargestellt. Also die gleiche Verteilung, sie sieht nur völlig anders aus. Magst du einmal beschreiben, wie das aussieht?

Janine: Ja. Beim ersten Histogramm waren es ja auch alle Pinguine, also nicht unterteilt in die Gruppen, das heißt, hier gibt es entsprechend auch nur eine Box für alle Pinguine. Auf der x-Achse ist in der Mitte 0,0, nach rechts gibt es noch 0,2 und 0,4 und nach links gibt es minus 0,2 und minus 0,4. Da habe ich keine Ahnung, was das sein soll und warum.

Helena: Ja, das ist da einfach nur, weil, naja, man muss ja irgendwie, wenn man so eine zweidimensionale Grafik berechnet, dann halt eben auch irgendwie x-Werte haben, wo man Dinge hinmalt. Die haben keine Funktion, die sind einfach nur da, die stehen einfach nur, die könnte man auch ausblenden, die sind nur eine Hilfe zum Grafikzeichnen.

Janine: Also es definiert quasi dein Raster.

Helena: Ja, genau. Es definiert nur das Raster, die haben keine inhaltliche Bedeutung.

Janine: Das macht sehr gut anschaulich, dass es hier tatsächlich eindimensionale Daten sind, glaube ich, oder?

Helena: Ja, gut. Aber dazu muss man in der Lage sein, die Zahlen zu ignorieren, die da halt trotzdem stehen,

Janine: Ja.

Helena: weil ich sie da nicht weggemacht habe, aber gleichzeitig ist es eben auch ein gutes Beispiel dafür, .a... dass nicht jede Information, die einem angezeigt wird, immer hilfreich ist.

Janine: Ja, jedenfalls auf der y-Achse ist dieses Mal die Flossengröße auch wieder in Millimeter, ich glaube, das habe ich beim letzten Mal vergessen zu sagen, angegeben, und zwar haben wir Werte von 170 bis knapp über 230, und die erste senkrechte Linie liegt auf der x-Achse auf 0,0, beginnt knapp über der 170 irgendwo und endet dort, wo die Box beginnt, bei dem Wert 190. Ja, die Box reicht dann bis ungefähr 213, 214, irgendwie sowas, das ist die Höhe der Box. Oben auf der Box beginnt dann eben direkt die zweite angesprochene Linie, die die oberen 25 Prozent der vorhandenen Daten anzeigt, auch wieder auf der Mitte der x-Achse und reicht bis über 230. Und ja, dann ist da eben das angesprochene fünfte Element, der Median, der liegt in der Box circa nach einem Drittel der Boxhöhe. Also, die Box ist irgendwie optisch in einen schmalen Streifen und einen breiteren Streifen dadrüber geteilt, und der Median verläuft irgendwo zwischen... joa... 197, würde ich mal sagen, aber die Mitte der Box, das sieht man ganz gut, wäre noch ein ganzes Stück höher.

Helena: Genau. Deswegen ergibt es eben auch 'n Sinn, diese Linie einzuzeichnen, weil die nicht immer in der Mitte sein muss. Und wenn die nicht in der Mitte ist, dann ist das auch ein Hinweis darauf, dass die Verteilung verschoben ist. Also, in diesem Fall haben wir zwei Pinguin-Arten, die eher kleiner sind und eine, die eher größer sind, und die sind alle zusammengepackt in diesem Plot, und entsprechend sind die meisten dann der Daten auch eher im unteren Bereich, und deswegen... ja, ist eben auch die Mittellinie nach unten verschoben, während oben dann nicht mehr, also da fasert es dann so ein bisschen aus. Da gibt es dann zwar immer noch genauso viele Pinguine oberhalb der Mittellinie, aber die verteilt sich auf einen größeren Größenbereich.

Janine: Ja, also kann auf jeden Fall gesagt werden, dass die häufigste Flossenlänge etwa 19,7 cm sind.

Helena: Äh, nicht die häufigste, das kannst du nicht aus diesem Plot draus lesen. Das, was man aus dem Plot lesen kann, ist, dass unter diesen 19,7 cm... die Hälfte aller Flossen sind kleiner und die andere Hälfte ist größer.

Janine: Ah, okay. Ich merke gerade, mein Kopf versucht ein zur Seite gekipptes Histogramm in diesen Boxplot zu legen.

Helena: Genau. Im Histogramm könnte man das eben sagen, die häufigste Flossenlänge ist folgende, wenn man jetzt Zentimeter-Schritte machen würde, was wir jetzt nicht gemacht haben, könnte man aber genau diese Aussage treffen, das ist die häufigste Flossenlänge in unserem Datensatz bei unseren Pinguinen. Aber hier geht das nicht, hier kann man nur sagen, wie viele sind größer und kleiner

Janine: Ja.

Helena: im Verhältnis zueinander.

Janine: Aber würdest du sagen, das macht dann quasi auch den Unterschied zwischen Histogramm und Boxplot aus, dass es... das Histogramm eher die Gruppe quasi in der Anzahl und der Häufigkeit beschreibt und der Boxplot die Gruppe eher, wie sie sich verteilt?

Helena: Also das, wie sie sich verteilt, beschreibt das Histogramm ja durchaus auch, aber der Boxplot ist mehr reduziert und sagt nur, wie die sich verteilt.

Janine: Ja, okay.

Helena: Und da spielt es gar keine Rolle mehr, wie oft, wie viele Pinguine wir eigentlich haben, weil das steht da nirgends.

Janine: Stimmt.

Helena: Und für viele Betrachtungen ist ja die Gesamtzahl auch gar nicht so wichtig, sondern eher die Verhältnisse untereinander. Und wenn das nicht relevant ist, lenkt es ja auch nur ab. Das ist halt der Vorteil am Boxplot, dadurch, dass es so reduziert ist, ist, wenn die Informationen, die man haben möchte, immer noch da sind, also wie verzerrt ist so eine Verteilung und so, und von wo bis wo geht die, dann ist die auch sehr nützlich, weil sie sehr deutlich sagt, wo ist so die Mitte der Größenverteilung und von wo bis wo geht die. Also die Mitte in einem Histogramm zu finden, das funktioniert, glaube ich, nicht ohne selber zu rechnen.

Janine: Ja.

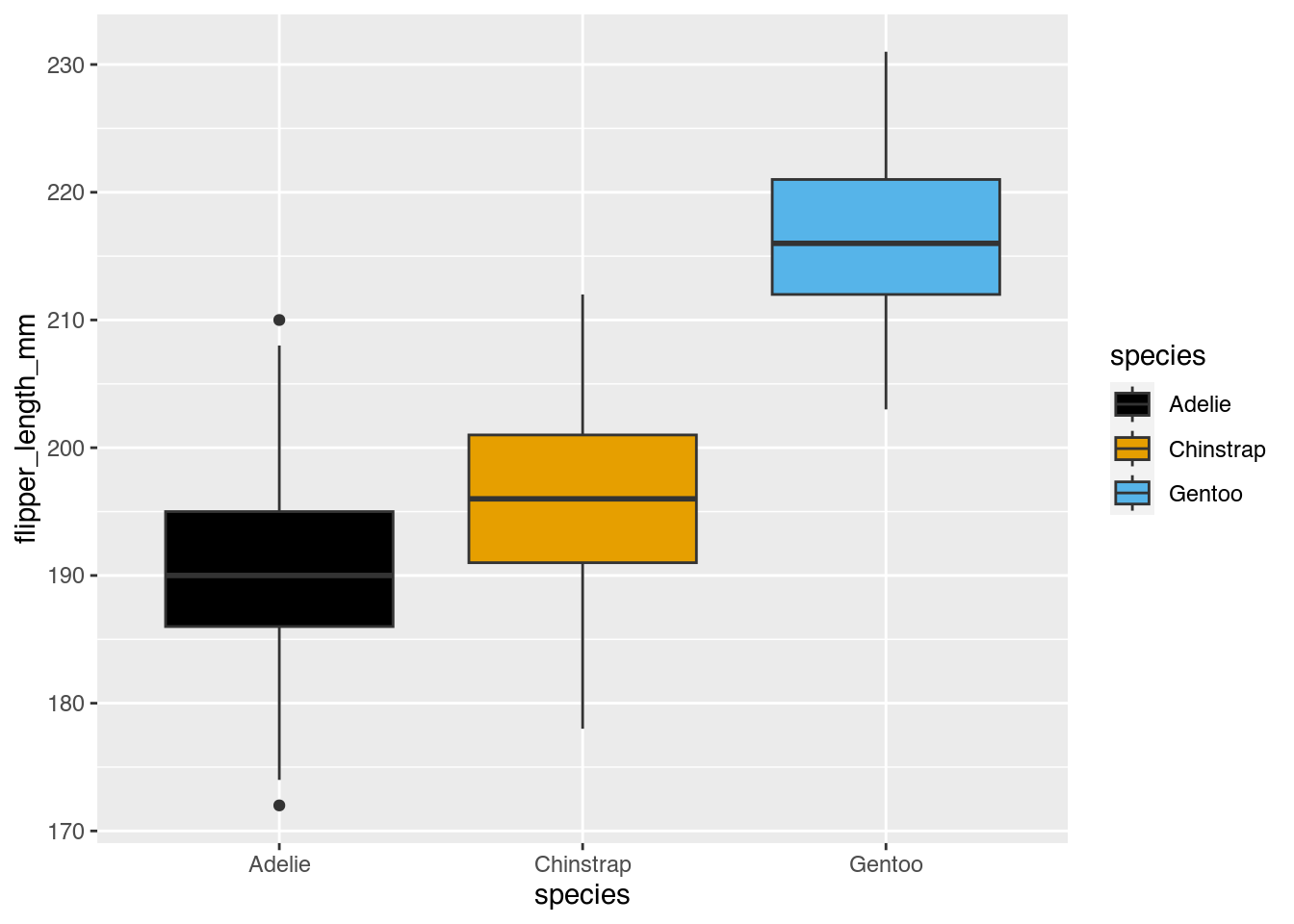
Helena: Dass man pro Pinguinspezies einen eigenen Plot gemacht hat, haben wir jetzt auch für die Boxplots gemacht. Möchtest du das auch noch mal beschreiben?

Janine: Ja. Hier haben wir einen Plot, der auf der x-Achse die Spezies der Pinguine hat. Da sind drei Boxen drin, die auch hier ihre eigene Farbe haben. Auf der y-Achse ist wieder die Flossengröße angegeben. Was hier jetzt erstmal ersichtlich ist, die Boxen sehen genauso aus wie vorher, vom Aufbau her. Bei den Adelie-Pinguinen gibt es tatsächlich unten und oben je einen schwarzen Punkt, bevor die Linie nach oben anfängt.

Helena: Genau. Das sind dann so Beispiele für diese Ausreißer. Also irgendwie gibt es einen sehr kleinen und einen sehr großen Pinguin, aber ich würde jetzt hier argumentieren, dass das Unsinn ist, die einzeln als Punkt darzustellen. Keine Ahnung, warum das Tool das jetzt gemacht hat. Die Linie hätte man doch einfach nur länger zeichnen können, hätte es auch nicht geschadet.

Janine: Ja, vielleicht als Beispiel oder so.

Helena: Ja.

Janine: Ja, was bei dieser ersten Gruppe auffällt, ist, dass der Median, der liegt auch nicht wirklich bei 50 Prozent, aber schon relativ nah dran. Also der untere Teil ist immer noch etwas kleiner, aber wirklich nur noch ein bisschen. Bei der Gruppe daneben, da beginnt die Box später circa ein Stück über dem Median der ersten Gruppe. Also die Boxen schweben quasi nebeneinander in dem Diagramm, wo die Adelie irgendwie von 70 bis 195 gehen oder so, da beginnt die Box der 50 Prozent der zweiten Gruppe bei 190 und endet irgendwie bei knapp über 200 und da ist der Median ziemlich mittig, finde ich.

Helena: Ja, finde ich auch.

Janine: Ja, die dritte Gruppe, da beginnt die Box deutlich weiter oben bei 212 und geht bis 220, ein bisschen drüber, die fängt fast an der Stelle an, wo der letzte Wert der Chinstrap-Gruppe überhaupt ist. Das macht den Abstand auch zwischen den Gruppen und den Pinguin-Größen, glaube ich, sehr gut deutlich.

Helena: Ja.

Janine: Der Median ist hier auch nicht ganz bei 50 Prozent, aber knapp darunter.

Helena: Ja, aber schon deutlich mittiger als in dem Boxplot, der alle drei Gruppen dargestellt hat. Genau, hier kann man dann auch sehen, dass die schon deutlich, ja, glockenkurviger verteilt sind, weil der Median deutlich mittiger liegt in der Box als noch in der Ursprungsgrafik. Das heißt, auch da kann man dann feststellen, ja, wenn jetzt irgendwie die Linie nicht ganz in der Mitte liegt, dann ist da irgendwas verzerrt und, ich meine, jetzt haben wir ja schöne Pinguindaten, das ist ja auch nicht immer so, dass die Daten so sind. Wenn man jetzt irgendwie Daten aufzeichnet, zum Beispiel digital, und dann hinterher so einen Boxplot macht, dann kann es auch schon mal passieren, dass die Box einfach nur eine Linie ist und dann hat die vielleicht oben oder unten noch eine Linie und dann ist alles sehr seltsam. Also, wenn die Box so eng ist, dass die Medianlinie und die Box quasi in eins verschmelzen, dann könnte es sein, dass irgendwie 90 Prozent der Daten einfach derselbe Wert sind. Und wenn man irgendwie ein Messverfahren hat, könnte das entweder heißen, man will auch, dass das immer konstant bleibt, dann ist das gut, oder die Messung ist kaputt. Und dass man so konstante Werte hat, ist ein Fehler und dann sollte man mal nachgucken, woran das liegt. Also, ich habe durchaus öfter mal, dass die nur noch eine Linie waren, gesehen und, ja, wenn da irgendwie 100 Datenpunkte denselben Wert haben und einer nicht, dann sieht so ein Boxplot auch sehr interessant aus, ... ist das eine Linie und dann gibt es irgendwo noch einen Punkt. Kann halt passieren, aber dann sollte man halt überlegen, was man machen will. Aber das ist ja auch durchaus hilfreich, dann zu wissen.

Janine: Also, würde ich sagen, hätten wir alles für den Boxplot zusammen, oder?

Helena: Ja.

Janine: Also, es ist nicht so sehr die Häufigkeit, sondern die Verteilung im Zentrum des Boxplots.

Helena: Ja.

Janine: Gut.

Was sind Violinenplots? (00:41:19)

Janine: Violinenplot hatte ich ja auch erwähnt und ich weiß von dir vor allem auch schon, dass das eine Variante des Boxplots ist. Was unterscheidet denn den Violinenplot vom Boxplot, beziehungsweise was sind denn die Vorzüge von dem?

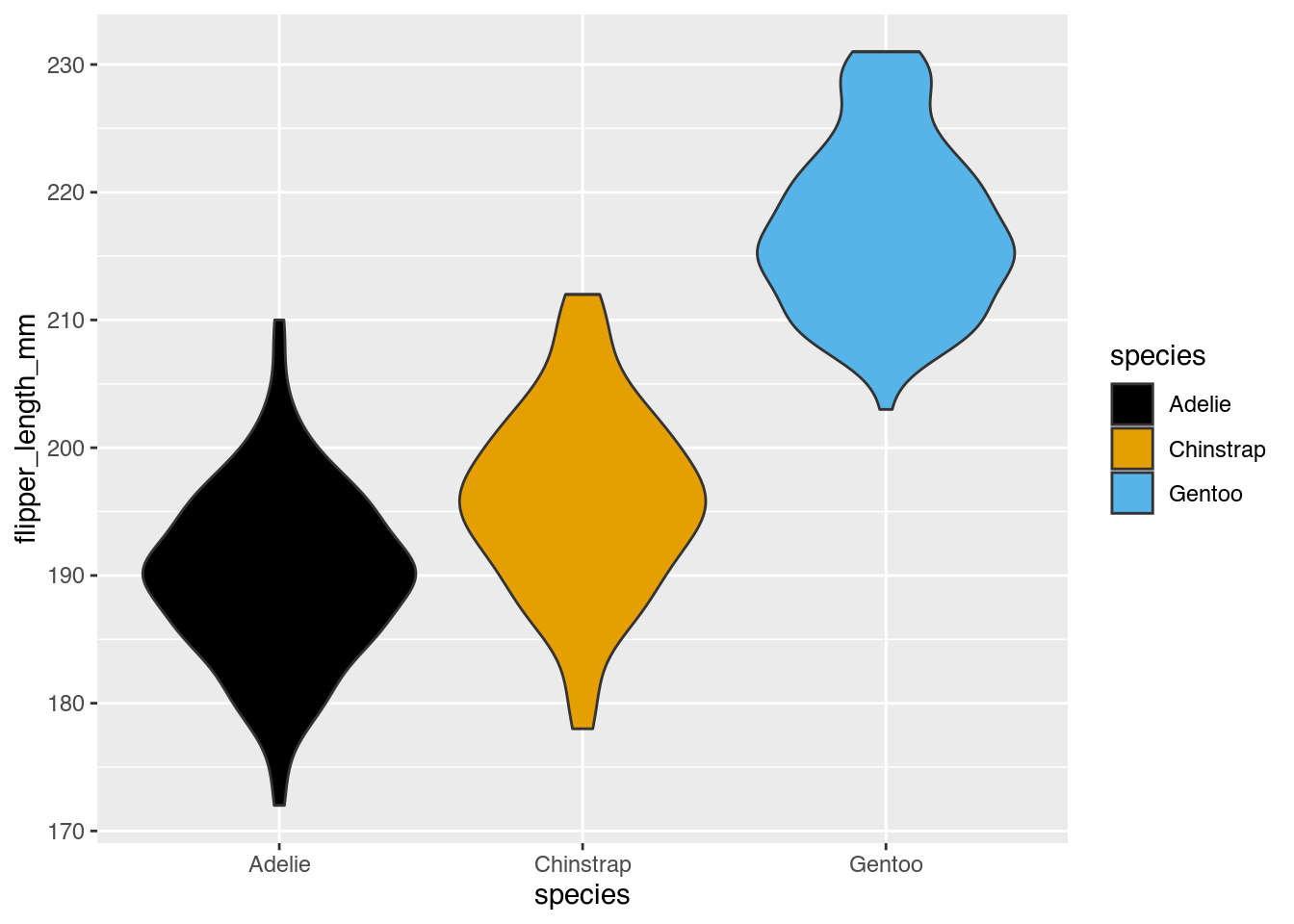
Helena: Also, beim Violinenplot kann man eben genau die gleichen Punkte darstellen, die ich gerade schon genannt hatte, also Median, 25 und 75 Prozent und Minimum und Maximum. Das, was sich unterscheidet, ist vor allen Dingen, dass die Box kein Rechteck mehr wird, sondern etwas, was potenziell so aussieht wie eine Violine, was so lustig geformt ist. Und was da im Wesentlichen passiert, ist, dass man über eine spezielle Berechnungsmethode quasi die relativen Häufigkeiten, so eine relative Verteilungsfunktion ausrechnet. Das heißt, die Violine ist dann besonders breit an den Stellen, wo auch viele Datenpunkte liegen. Man könnte das vielleicht wie eine Mischung aus Boxplot und Histogramm sehen, nur dass die genaue Häufigkeit nicht gesagt wird, sondern man nur ein relatives Gefühl dafür bekommt, wo liegen mehr der Daten, wo weniger der Daten, weil die eben so breiter wird, wo viele Daten liegen und schmal ist, wo wenig Daten liegen. Und im Prinzip ist das, was man da als Verteilungsfunktion ausrechnet, was dann eben die Breite darstellt, das wird dann auch gespiegelt, sodass das dann symmetrisch wie eine Violine aussieht. Und man kann dann eben, wie gesagt, auch Medialen und die beiden Linien oben und unten einzeichnen. In unserem Beispiel haben wir das nicht gemacht. Dafür, ja, sieht man eben, dass die Bäuche unterschiedlich liegen.

Janine: Ja, bei dem Plot ist es auch wieder so, dass die Adelie und die Chinstrip-Pinguine relativ nah beieinander sieht, aber man erkennt hier halt tatsächlich besser als beim Boxplot, finde ich, dass irgendwie, ja, der Median ein bisschen übereinander liegt. Und ich finde so, die Boxplots, also dadurch, dass es wirklich Rechtecke sind, die da reingemacht werden in den Plot, ja, die verschleiern das irgendwie so ein bisschen. Die geben irgendwie das Gefühl einer homogenen Gruppe von 50 Prozent, die alle gleich sind und dann wird da halt nur der Median eingezeichnet, um das zu relativieren. Und hier sieht man das tatsächlich durch die Form des Violinenplots. Und auch hier ist es so, dass die Gentoo-Pinguine deutlich weiter oben erst anfangen und der Median da auch viel höher liegt als überhaupt die Violinen der anderen beiden Gruppen.

Helena: Genau, Violinenplots sind eben eine, ja, moderne Variante von Boxplot, die halt ein bisschen mehr Infos gibt. Ein Vorteil von Boxplots, den ich an der Stelle vergessen habe, ist allerdings, dadurch, dass das immer die gleichen fünf Werte sind, die man darstellt, kann man das auch einfach tabellarisch darstellen. Man könnte auch einfach komplett die Grafik weglassen und einfach nur eine Tabelle vorlesen. Das kann insofern helfen, als dass es immerhin schon mal sagt, wie man das erklären soll, während Histogramme und Violinenplots durch ihre Form ja deutlich schwerer auch zu beschreiben sind, wenn man das nur auditiv erklären kann.

Janine: Ja.

Helena: Gut, ich meine, wir haben jetzt die Tabelle trotzdem nicht vorgelesen, weil es jetzt auch gar nicht um die konkreten Zahlen so sehr geht, sondern mehr um das Gefühl, was sie vermitteln. Aber es ist bei Boxplots immerhin möglich.

Janine: Okay, also wäre sozusagen die Zusammenfassung für den Violinenplot, dass durch die spezifische Form, dass es eben auch je nach Datenlage schmaler und breiter werden kann, ja, eigentlich eben ein bisschen besser die eigentliche Datengrundlage mit sichtbar ist, also wovon habe ich mehr?

Helena: Mhm.

Janine: Und dadurch, ja, es ist nicht ganz so begrenzt wie der Boxplot, wobei begrenzt natürlich jetzt negativ klingt. Es ist eben, ja, die Frage, was man zeigen und sehen möchte, und deswegen, ja, der Violinenplot bietet halt mehr Optionen für eine weitere Interpretation dann sozusagen.

Helena: Ja, und es ist kompakter darzustellen als jetzt so ein Histogramm. Histogramm ist recht groß.

Janine: Ja.

Helena: Und hier kann man die halt deutlich kompakter, die verschiedenen Kategorien darstellen. Und, ja.

Janine: Ich glaube, dann hätten wir das mit dieser Form der Plots.

Was ist kumulierte Häufigkeit? (00:45:46)

Janine: Ich hatte noch eine vierte Sache genannt, die kumulierte Häufigkeit. Was zum… ist das?

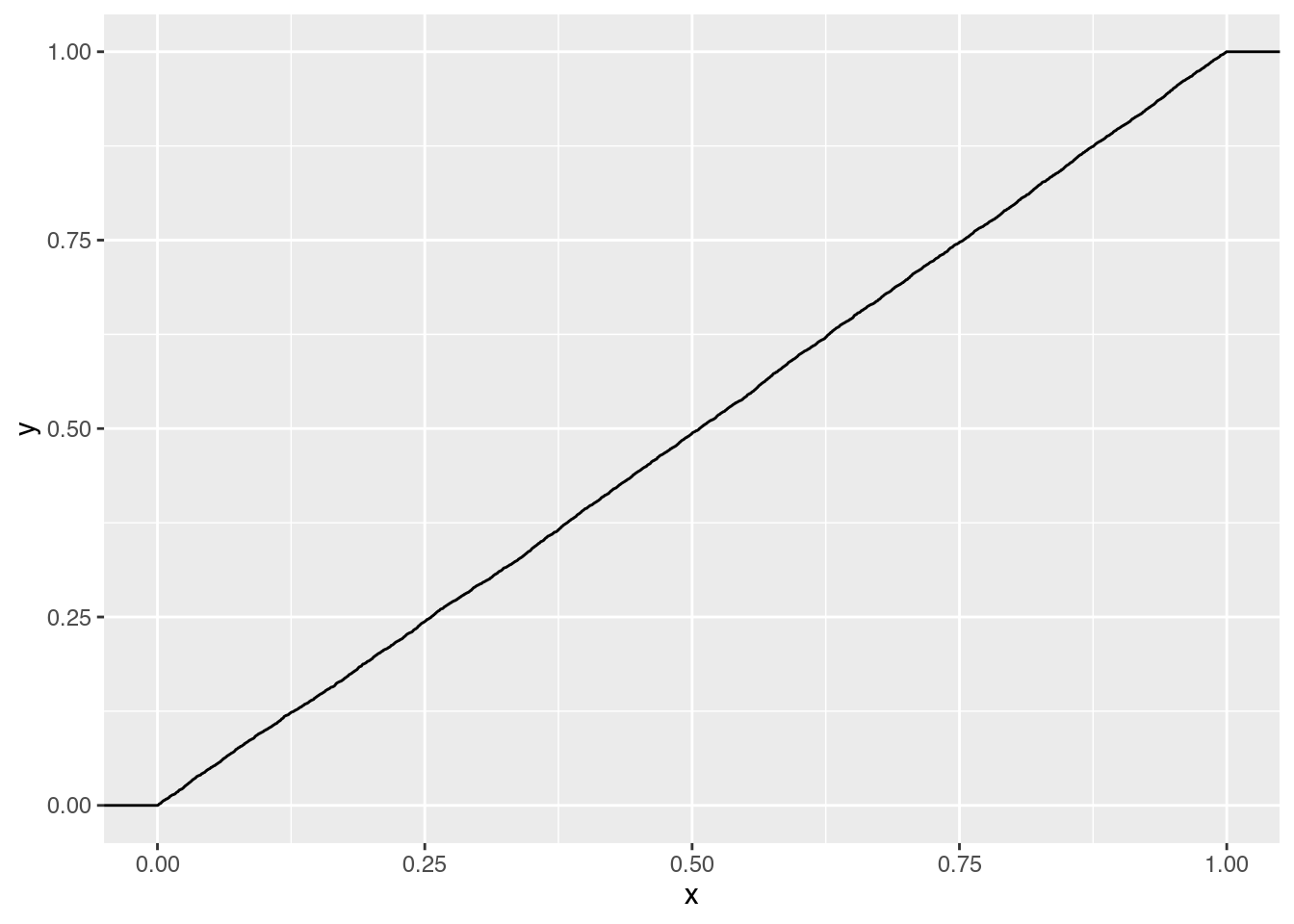
Helena: Genau, das erste Wort kumuliert oder auch aufsummiert ist, wenn man nicht immer jeden einzelnen Datenpunkt für sich nimmt, sondern wenn man quasi einen Haufen Daten hat, und das, was man sich anguckt, ist aber die Summe, dass man quasi den ersten Datenpunkt nimmt, dann den ersten plus den zweiten, dann den ersten plus den zweiten plus den dritten, und dass es dann immer nur nach oben geht. Im Grunde ist so ein aufsummierter Wert auch genau das Beispiel aus dem Stromzähler, weil viele Stromzähler laufen eben nicht rückwärts und typischerweise gehen ja nur in eine Richtung und zählen nur hoch. Und um dann wiederum den einzelnen Wert auszurechnen, müsste man eben jeden Tag ablesen und voneinander abziehen für den Tageswert. Ansonsten plottet man auch immer nur eine Linie, die immer nur hoch geht. Wir haben ja auch vor kurzem angefangen, ein paar unserer Folgen und Inhalte auch auf YouTube hochzuladen, und dort gibt es auch eine Grafik, die dann die Statistik macht, ja, wann wurde das Video wie oft geschaut, und das ist dann auch eine kumulierte Grafik, das heißt, die zeigt dann immer nur eine Linie, die hoch geht. Unterschiedlich stark, je nachdem, wie oft das geguckt wurde an den Zeitraum, kann das mal steiler hochgehen und flacher hochgehen, aber es geht immer nur hoch, es kann nicht wieder runtergehen. Das sind eben aufsummierte Werte oder kumulierte Werte. Und bei der kumulierten Häufigkeit macht man jetzt aber, bevor man das aufzeichnet, noch einen Schritt, und zwar sortiert man alle Werte durch, dass man quasi alle Flossen unten stehen hat, die klein sind, und dann zählt, ja, wie oft ist denn diese Flossenlänge vorgekommen, wie oft ist die nächste vorgekommen. Also auch hier zählt man wieder, so ähnlich wie bei einem Histogramm, nur dass man jetzt wirklich nicht mehr Werte zusammenfasst, sondern nur die Werte zusammenfasst, die auch wirklich den gleichen Wert haben. Also wenn jetzt irgendwie 18 cm jetzt dreimal vorgekommen ist, dann würde man das jetzt auch zusammenzählen, aber im Grunde genommen fällt man dann quasi bei 0 an und geht dann hoch bis zu der Gesamtanzahl an Pinguinen, beziehungsweise in der Darstellung, die wir jetzt auch in den Shownotes haben, teilt man dann auch durch die Gesamtzahl der Pinguine, das heißt, es fängt bei 0 an, es gibt 0 Pinguine, die kleiner sind als 170 mm oder 17 cm, keine Pinguine, die größer sind als 23 cm.

Janine: Beziehungsweise deren Flossen.

Helena: Genau, deren Flossen.

Janine: Das wäre so niedlich, Pinguine, die 23 cm groß sind, ausgewachsen.

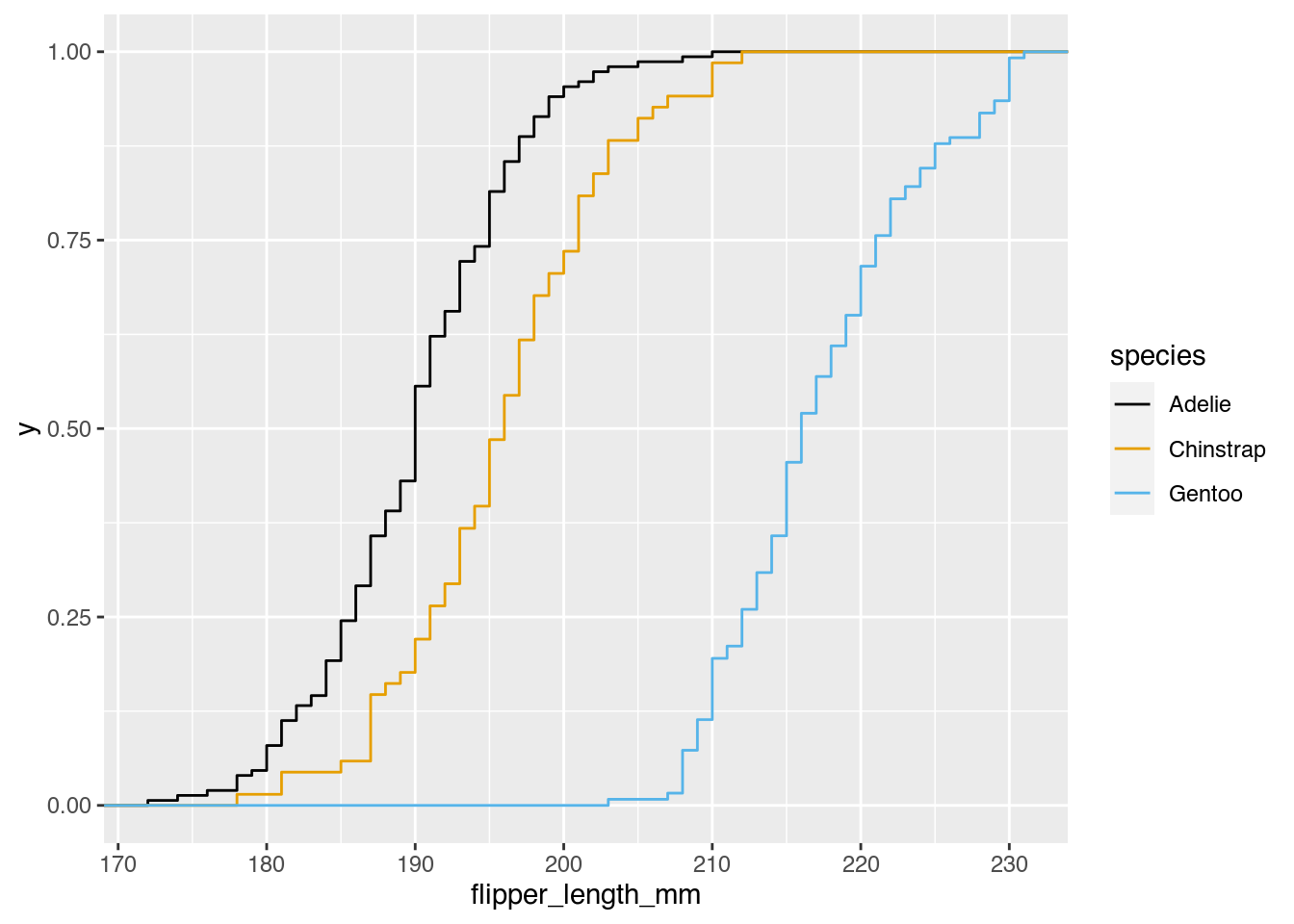
Helena: Das stimmt. Jetzt könnte man natürlich auch die y-Achse nochmal 100 rechnen, um Prozent zu haben, also 50 % der Pinguine sind dann kleiner und 50 % sind größer. Aber auch hier kann man eben die Verteilung relativ gut sehen und hier, wenn man sich jetzt diese Grafik anguckt, dann ist das so ein Treppenstufenartig und die Stufen sind halt steiler, wenn für diesen Wert mehr Werte existieren und das fängt irgendwie relativ flach an und dann kommen ganz steile Treppenstufen und dann wird es wieder flacher und irgendwann hört es halt auf. Wenn der Wert bei 1 angekommen ist, ist es halt auch Ende.

Janine: Ja, es sieht aus wie so quasi drei S, die da nebeneinander gesetzt wurden.

Helena: Ja, und was man jetzt eben sagen kann, ist so, man sieht jetzt hier eine Linie für die Adelie-Pinguine und da sieht man ja 50 % der Adelie-Pinguine sind kleiner als 190 mm. Ich meine, das sieht man auch aus dem Boxplot.

Janine: Ja.

Helena: Was man jetzt hier aber auch machen kann, ist, man geht dann bei diesen 190 weiter runter bis zu den Zügel-Pinguinen und sieht dann, ah, okay, da ist die Linie bei 20 %, das heißt 20 % der Zügel-Pinguine sind kleiner als 19 cm, also deren Flossen sind kleiner als 19 cm.

Janine: Ja.

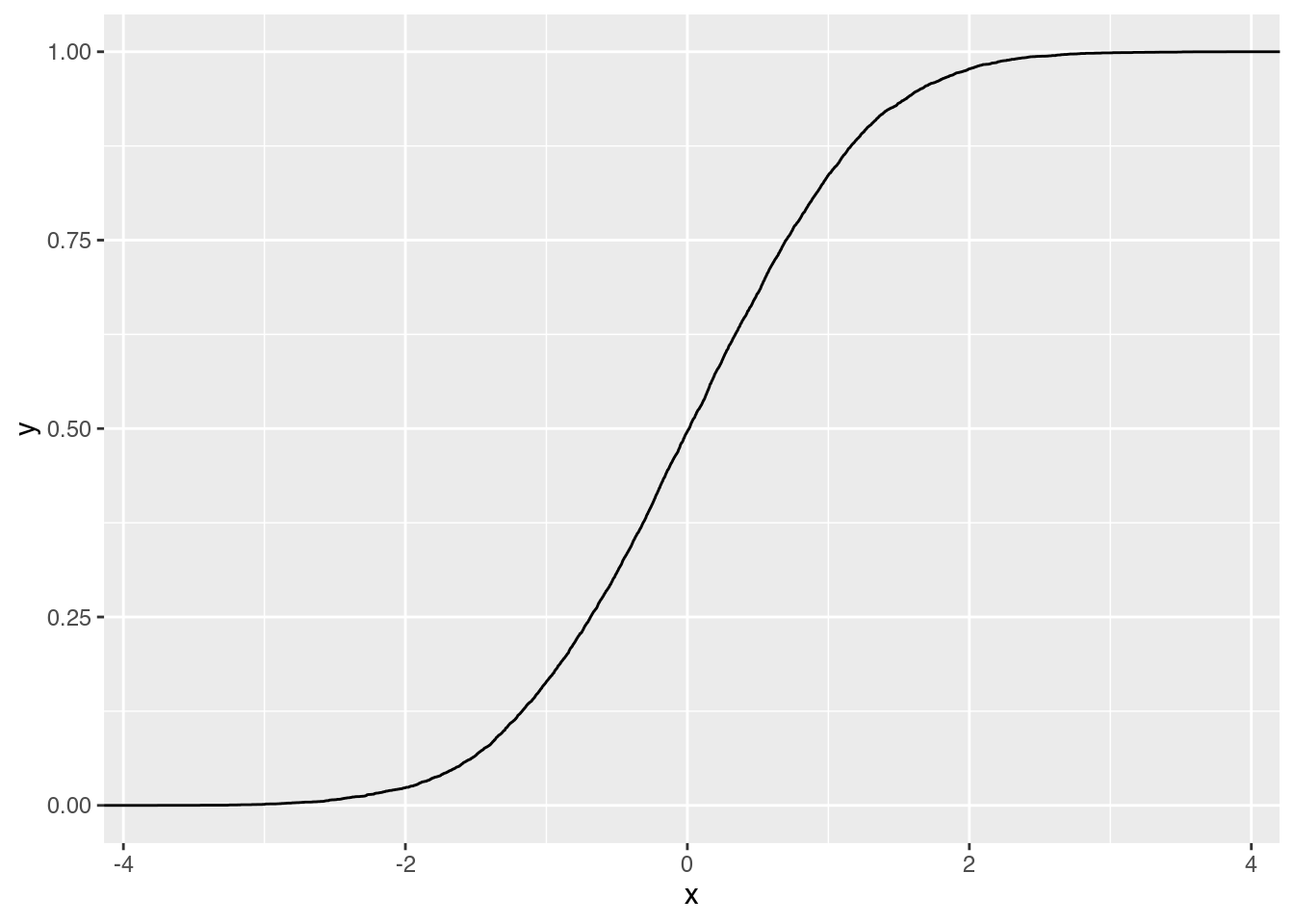
Helena: Dadurch lassen sich deutlich besser diese Größen vergleichen, so die Größenverteilung vergleichen und eine konkrete Aussage treffen, auch für Punkte, die jetzt nicht im Boxplot eingezeichnet sind. Ich meine, im Boxplot ist 25 eingezeichnet und 25 ist hier auch eingezeichnet, aber eben auch die ganzen Werte dazwischen kann man hier ablesen. Wenn man sowas jetzt zum Beispiel für Schulnoten machen würde, dass man dann sagt, ja, so viele haben mindestens eine 4 geschrieben und so viele haben vielleicht eine 1, da kann man sagen, ja, irgendwie 50 % der Leute waren besser als eine 2 und das könnte man auch relativ schnell sagen, aber eben auch für die Zwischenwerte. Und hier sieht man auch, dass im Grunde da, wo die Adelie-Pinguine und die Zügel-Pinguine, deren Flossengröße ungefähr aufhört, da fangen die von den Gentoo-Pinguinen gerade erst an. So, es gibt leicht Überlappungen, aber die stehen gar nicht so im Vordergrund, sondern es ist eher... im Vordergrund stehen weniger die Überlappungen als die einzelnen Werte, die man sehr deutlich ablesen kann. Und, was man eben auch noch machen kann, ist, also wir haben jetzt in den Shownotes auch noch zwei weitere Grafiken, das eine sieht dann deutlich mehr aus wie so ein S, also so eine logistische Kurve, die leicht ansteigt, dann steil wird und dann leicht abflacht. Und das ist das, was man erwarten würde eben bei so einer normal verteilten Größe, also bei so einer Glockenkurve, die wir jetzt schon öfter erwähnt hatten. Und ein Beispiel, was einfach nur eine gerade Linie ist. Und so eine gerade Linie ist das, was rauskommt, wenn jeder Wert gleich oft vorkommt. Also im Prinzip würde man so eine gerade Linie oder eben so eine gerade Linie, die man so eine gleichmäßige Treppe, die nicht irgendwie abflacht, außer da, wo die Werte nicht mehr existieren vielleicht, wäre auch das, was man bei einem Würfel erwarten würde. Also wenn man jetzt so einen 20-seitigen Würfel hat, sollte ja jeder Wert gleich oft vorkommen und würde man das jetzt eben auf diese Art darstellen, müsste da im Prinzip eine gleichmäßige Treppe bzw. eine gleichmäßige Linie, wenn man da eine Linie durchzeichnet, rauskommen, die nicht irgendwie erst abflacht und steiler wird und so weiter. Und wenn die steiler wird zwischendurch, dann ist der Würfel vielleicht nicht präzise. Nicht fair.

Janine: Dann steht da so was wie 1, 2, 3, 4, 4, 4, 5, 6, 7, ja?

Helena: Das würde man dann in dieser grafischen Darstellung sehr schnell sehen, dass der Würfel unfair ist.

Janine: Gezinkt.

Helena: Ja.

Janine: Achso, okay. Also die kumulierte Häufigkeit eignet sich zum Erfassen von Schumlern beim Würfeln.

Helena: Ja, zum Beispiel.

Janine: Ja, gut, tatsächlich fällt mir einfach zu diesem Plot gar nichts ein. Wobei du hast gesagt, dann würde man ziemlich schnell sehen, dass da etwas nicht richtig ist. Wir hatten ja in Folge 13 über Datenvisualisierung gesprochen und wofür die eingesetzt werden können. Also was die Ziele der Darstellung sein können. Und da hatten wir erwähnt, dass es Exploration, Kommunikation und Verifikation gibt.

Helena: Ja.

Janine: Also Exploration, das Erkunden von Datensätzen mittels Grafiken, Kommunikation, eben das Darstellen eines Datensatzes für ein weiteres Publikum, also die.. das Ergebnis sozusagen zu kommunizieren und Verifikation, um, ja, zu überprüfen, ob man auf dem richtigen Weg ist, sozusagen. Ich glaube, du hattest es mit Modellen dann erklärt, passt mein Modell, was sagen die Daten, wie passt das zusammen?

Helena: Genau.

Janine: Würdest du sagen, dass sich jetzt die kumulierte Häufigkeit da besonders gut eignet, um da bestimmte Sachen hinsichtlich von Explorationen oder eben Verifikation zu machen?

Helena: Ja, das eignet sich vor allen Dingen für sowas wie Verifikation, also gucken, ob das Modell stimmt. Ich hatte ja schon bei den Histogrammen gesagt, dass man die Daten ganz gut nutzen kann, um jetzt sowas wie eine Gauß'sche-Glockenkurve reinzumalen, reinzufitten, also so ein Modell daran anzupassen. Aber dann hängt es ja immer noch davon ab, wie ich die Balkenbreite gewählt habe, wie dann halt auch so der Skalierungsfaktor für die Verteilung aussieht. Es gibt auch für die Gauß'sche-Glockenkurve ein kumuliertes Modell, was dann mathematisch gesprochen einfach das Integral ist darüber, und das ist auch eine eigene Funktion, das ist dann die sogenannte Fehlerfunktion. Im Prinzip basiert die einfach nur auf denselben Infos wie die Glockenkurve, nur halt ist eine andere Darstellung davon, und die könnte man jetzt einfach auch noch hier reinmalen in diese kumulierte Häufigkeit, und dann würde man sehen, ja, liegt die auch an der gleichen Stelle, überlappen die sich gut.

Janine: Mhm.

Helena: Und das könnte man hiermit halt einfacher machen als mit so einem Histogramm, auch wenn ein Histogramm trotzdem erstmal einfacher zu lesen wäre. Wenn man eine Glocke reinmalt, ist das auch erstmal irgendwie nachvollziehbarer. Aber man muss halt eigentlich mathematisch sogar noch mehr Anpassung vornehmen, um halt für die Breite der Balken zu kompensieren, deswegen ist das insofern etwas unelegant als wenn man halt einfach nur die Fehlerfunktion in diese wunderschönen kumulierten Häufigkeiten reinmalt.

Janine: Und du hattest ja auch bei Histogrammen und Boxplots und so, glaube ich, auch relativ häufig das Wort Gefühl benutzt, also dass man ein Gefühl dafür kriegt, wenn man sich die anguckt. Ich denke, die passen dann wahrscheinlich auch am ehesten zu der Exploration.

Helena: Ja, also dafür sind die sehr nützlich. Also, um einfach ein Gefühl für die Daten zu bekommen, finde ich all diese Plotarten gleichermaßen hilfreich. Zur Kommunikation ist es ja sehr zielgruppenabhängig, wenn man weiß, die Leute benutzen gerne Boxplots oder Violinplots, dann kann man das wunderbar benutzen, und auf jeden Fall sollte man das dann auch tun, wenn man jetzt eher an die allgemeine Öffentlichkeit geht, dann sind eigentlich nur die Histogramme relevant zur Kommunikation, weil die anderen müsste man ja erstmal erklären. Also, ich meine, ich finde es immer noch gut, wenn man auch Bass benutzt, wenn es halt die bessere Darstellung ist für das, was man haben will, aber da muss man mehr erklären, und deswegen sind für Kommunikation Histogramme halt deutlich niederschwelliger.

Janine: Klingt einleuchtend.

Wie am besten Plots mit R erstellen? (00:56:14)

Janine: Ja, gut, dann hätten wir es soweit mit all den verschiedenen Formen, und ich würde sagen, wir schleichen rüber zum Fazit, aber ich weiß, dass du da noch ein bestimmtes Fazit quasi vorweg geben willst. Also, es sind ja alle Plots in unseren Shownotes selbst erstellt, und ich glaube, das Erstellen dieser Plots hat schon zu einem eigenen Fazit geführt.

Helena: Ja, genau, also ich benutze R für sowas, und in R gibt es ein wunderbares Tool namens ggplot, mit dem man einfach Plots generiert, die einfach von Anfang an hübsch aussehen, die gut lesbar sind, die haben auch immer diesen leicht grauen Hintergrund, damit der Kontrast zwischen einer weißen Oberfläche und der schwarzen Schrift nicht so groß ist und das angenehmer ist fürs Auge, je nachdem, wo man es darstellt, und das macht schon eine ganze Menge richtig und nimmt einem auch eine ganze Menge Arbeit ab, was das Plotten angeht. Wenn ich jetzt allerdings im Internet gucke an Beispielen für R, dann finde ich immer, dass da die Standard-Plot-Funktionen für Histogramme oder Boxplots erwähnt werden, die in dem originalen R schon vorhanden waren, und die funktionieren auch, aber die sind nicht besonders optisch ansprechend, finde ich, und ich verstehe nicht, warum, obwohl ggplot schon seit über zehn Jahren im Einsatz ist, man immer noch diese anderen Funktionen findet in irgendwelchen Vorlesungsskripten im Internet oder auf YouTube. Ich meine, ja, das geht schnell, und für den allerersten Überblick ist es oft auch schneller, als erstmal ggplot zu laden, aber es lohnt sich die Zeit zu investieren in ggplot zu lernen, weil man kriegt so viel hübschere und mächtigere Plots hin, dass sich das sehr schnell lohnt.

Janine: Woher weiß ich denn, was sozusagen die moderne Best-Practice ist, also vielleicht ist ggplot ja irgendwann auch mal überholt. Gibt es irgendetwas bei R, was einen gewissen Standard setzt, also in Internet-Dingen gibt es das W3-Konsortium, wie ist das bei R?

Helena: Ja, bei R gibt es ja außer der eigentlichen Sprache selber, die halt historisch gewachsen einige Inkonsistenzen hat, mittlerweile sehr viele Zusatzpakete, und insbesondere das sogenannte Tidyverse, sei hier zu nennen, das ist so eine Zusammenstellung von ganz vielen Paketen, die deutlich konsistentere Datenstrukturen haben, wo sich nicht einfach plötzlich mal der Datentyp ändert, wenn man was macht, nur weil zufälligerweise die Zahl, die man reinschreibt, in der einen Fall 0 und in der anderen 2 ist, ja, kann ich da auf jeden Fall empfehlen, und da gibt es auch ein sehr gutes Buch namens R for Data Science, das gibt es auch komplett online zu lesen, man kann sich das aber auch kaufen, da stehen all diese Tools auch drin, und ansonsten verlinken wir noch das Tidyverse, wo eben nicht nur ggplot mit drin ist, sondern eben auch noch ein paar andere ziemlich coole Funktionen, die ich auch in meinem beruflichen Alltag sehr viel verwende.

Janine: Sehr gutj

Fazit (00:59:18)

Janine: Dann das richtige Fazit, was ist denn so das Fazit, das wir hier ziehen?

Helena: Ja, also mein Fazit ist, Histogramme sind ein gutes Tool, um Überblick über eine Datenmenge zu bekommen, und es ist auch gut verständlich, um die Daten zu kommunizieren, Boxplots sind noch reduzierter und auch gut für Übersicht, aber man verliert eben an Genauigkeit, manchmal ist das auch angemessen, manchmal nicht, und ja, die aufsummierten Häufigkeiten, also, ja, die kumulierten Häufigkeiten, die muss man erstmal ein bisschen lernen, damit umzugehen, aber auch dann kann man da sehr schöne Informationen rausziehen.

Janine: Ich nehme auf jeden Fall mit und möchte als Fazit nochmal betonen, dass der Grund, warum oder was ich mit bestimmten Daten mache, die Dimensionalität meiner Datenpunkte ausmacht, also wie viele Dimensionen meiner Daten benutze ich eigentlich, wenn ich nur eine Dimension benutze, dann ist es eben der Ausgangspunkt quasi ein eindimensionaler Datensatz, und ja, ich kann eindimensionale Daten aber in zweidimensionalen Grafiken darstellen.

Helena: Ja.

Janine: Und der Punkt, den Helena da gemacht hat, war eben, dass ich das eine Mal meinen Messwert habe und die andere Dimension in dieser Grafik nicht einen gemessenen Wert darstellt, sondern einen Wert, den ich aus der ursprünglichen Messung ableiten kann, den ich berechnen oder erzeugen kann, auf welchem Weg auch immer, und deswegen bleibt, obwohl es zweidimensional dargestellt ist, diese Grafik eine Darstellung von einer eindimensionalen Verteilung.

Helena: Genau.

Janine: Und wenn man dann wieder so Sachen macht, wie bestimmte Tage oder Zeitpunkte reinzubringen, obwohl ich etwas anderes gemessen habe, dann habe ich eben aus meinem Datensatz schwupps einen zweidimensionalen gemacht.

Helena: Was dann zu der Frage führt…

Janine: Was ist der nächste Schritt?

Helena: Genau. Nach eindimensionalen Verteilungen ist dann die Frage, was ist denn so mit mehr dimensionalen Daten? Und schon bei zweidimensionalen Daten wird es komplizierter, weil die Frage ist, was ist denn jetzt die zweite Dimension? Und es gibt eine, die sehr bedeutsam ist, nämlich die Zeit. Sobald man eine Größe über die Zeit aufträgt, hat man ja auch zwei Dimensionen, Zeit und keine Ahnung, Stromspeicherwert, und sobald die Zeit dann eben auch eine Rolle spielt, spricht man von einer Zeitreihe, das heißt, eine Folge wird sich bestimmt in der Zukunft über Zeitreihen gehen und was man damit machen kann. Aber es gibt auch andere Arten von mehrdimensionalen Daten, sowas wie Ortsdaten, wo man dann Geokoordinaten hat, so Länge und Breite, oder von Gebäudedaten hat man vielleicht sogar drei Dimensionen, wenn man dann die Länge, Breite und Höhe hat, das kann beliebig kompliziert werden, aber auch sehr nützlich.

Janine: Ja, ich bin gespannt drauf, vor allem bin ich drauf gespannt, weiter in die Zukunft geguckt, wie lang diese Reihe wird und welchen Komplexitätsgrad wir erreichen werden.

Helena: Da bin ich auch gespannt.

Nächste Folge: Überraschungsfolge am 22. April 2023 (01:02:28)

Helena: Aber die nächste Folge wird sich jetzt noch nicht um Zeitreihen drehen, wir schauen mal, wann das gut reinpasst. Trotzdem wissen wir noch nicht, worum es in der nächsten Folge geht, deswegen wird die Überraschungsfolge am 22. April erscheinen, da wir diesmal ja aus Termingründen früh aufnehmen und uns noch nicht entschieden haben, was das nächste Thema sein wird. Also wir haben viele Themen zur Auswahl, aber was wir nehmen, schauen wir mal, ihr werdet sehen.

Call to Action (01:02:56)

Janine: Genau. Und wenn ihr das sehen beziehungsweise vor allem hören wollt, dann folgt uns doch auf Mastodon unter (at) datenleben@podcasts.social oder auf Twitter unter (at) datenleben. Besucht gerne unsere Webseite www.datenleben.de, manchmal erscheinen da auch Blogposts und wie Helena schon sagte, wir sind jetzt auch auf YouTube und versuchen da ein bisschen Content reinzubringen. Guckt doch gerne mal vorbei, ob euch das gefällt, was wir da machen und hinterlasst uns zu allem gerne Feedback. Wir freuen uns immer sehr darüber, falls ihr uns als Data Scientist buchen wollt für Analysen oder Projekte, dann schreibt auch das gerne und falls ihr Fragen oder Themen habt, die euch interessieren, dann, ja, ihr kennt unsere Kontakte.

Helena: Dann bleibt mir nur noch für eure Aufmerksamkeit zu danken und bis zum nächsten Mal. Ciao.

Janine: Tschüss.

Outro (01:03:50)