dl029: graphentypen – skalen und zeiger

Intro (00:00:00)

Thema des Podcasts (00:00:18)

Willkommen zur neunundzwanzigsten Folge beim datenleben-Podcast, dem Podcast über Data Science.
Wir sind Helena und Janine und möchten euch die Welt der Daten näher bringen.
Was für Daten umgeben uns? Wie werden Daten für uns lesbar? Und was können wir aus ihnen lernen?
Wer schon immer mehr darüber wissen wollte, ist hier richtig, denn diesen Fragen gehen wir nach.

Thema der Folge (00:00:41)

Wir haben in der Folge 13 allgemein über Datenvisualisierung gesprochen und was für Gründe es geben kann Daten zu visualieseren
Daran wollen wir nochmal anknüpfen und auch mal wieder data science "tools" fokussieren
In dieser Folge soll es darum gehen, was es für konkrete Arten von Darstellungen für Daten gibt
Aber das ist ehrlich gesagt ein ziemlich umfangreiches Thema
Deswegen ist das mit recht hoher Wahrscheinlichkeit nur der Auftakt zu einer ganzen Reihe dazu
Es gibt so viele verschiedene Datentypen und damit auch so viele Optionen, sie darzustellen, dass wir das nach und nach ergänzen möchten
Wir wollen in dieser Folge klein anfangen und haben uns quasi eine der kleinsten Einheiten rausgesucht: 1-dimenionale Daten
Genauer gesagt: Wie stellt man einen einzigen Wert dar? Was gibt es für Möglichkeiten?

Warum ist das Thema interessant? (00:01:54)

Bei 1-dimensionalen Daten gibt es auch die Variante, dass man ganz viele davon hat
Im Gegensatz zu nur einem ganz aktuellen Wert
Und dann gibt es noch die Möglichkeit, außer so einer Verteilung von Daten, dass man einen weiteren Wert hat, was 2-dimensionale Daten sein können
Aber da das geht beliebig kompliziert, deswegen fangen wir an, das von Anfang an aufzurollen

Einspieler: Was sind Daten? (00:02:36)

Was sind Daten?
Wir reden hier über Data Science, also gewissermaßen Datenwissenschaft, die Wissenschaft von und oder über Daten.
Eigentlich kennen wir alle den Begriff Datum, auf den der heutige Daten-Begriff zurückgeht, eher als eine ganz bestimmte Angabe, wie zum Beispiel: 18.08.2022 (was das Datum der heutigen Aufnahme ist)

In der Bedeutung ‘gegebene Größe, Angabe, Beleg’ wird das bereits im Lat. substantivierte Partizip (lat. datum n. ‘das Gegebene, Gabe’) meist in pluralischer Form von der Wissenschaftssprache des 17. Jhs., vornehmlich des 18. Jhs. aufgegriffen. Seit Beginn des 19. Jhs. tritt in dieser Verwendung neben die lat. Pluralform Data verstärkt der eingedeutschte Plur. Daten, der sich im 20. Jh. durchsetzt und seit den 50er Jahren als Bestimmungswort zahlreicher Zusammensetzungen wie Datenverarbeitung, Datenbank dient. Quelle
Wegen dieser Überschneidung sprechen wir bei einzelnen Daten übrigens nicht vom Datum, wie für eine Datumsangabe, sondern eher von einem Datenpunkt
Wir benutzen sie sogar: Wenn wir uns etwas ansehen, etwas lesen, etwas zählen, etwas entscheiden
Dafür müssen wir die Daten allerdings interpretieren, weder einzelen Datenpunkte noch ganze Datensätze oder -sammlungen haben für sich genommen eine Aussage
Sie müssen von uns in ein Verhältnis zu etwas gesetzt werden, wodurch wir aus einzelnen Daten schließlich Informationen gewinnen
Und diese brauchen wir, um darüber zu entscheiden, was wir tun, ob etwas richtig oder falsch, gut, gesund oder ungesund, zu heiß oder zu kalt ist
Dem wert ist es egal, ob 18 grad zu kalt oder genau richtig sind, es sind einfach eben 18 Grad.
Den Menschen wiederum interessiert es, was diese 18 Grad bedeuten und durch den Kontext können wir die Daten interpretieren und Informationen gewinnen
Und um diese Bedeutung zu erfassen, müssen die Daten entsprechend dargestellt werden
Daten und das, was sie an Informationen vermitteln wollen, müssen zusammen passen und sie müssen verständlich sein

Was heißt eigentlich Dimension bei Daten? (00:06:06)

In Folge 13 haben wir allgemein über Datenvisualisierung gesprochen und was für Gründe es geben kann diese Daten zu visualieseren
Wir 3 Punkte benannt: Exploration (Überblick), Kommunikation (Vermitteln) und Verifikation (Überprüfen)
Jetzt wollen wir konkrete Arten von Daten und Darstellungen angucken, hier: wenn sie nur einen einzelnen Wert haben
Was heißt 1-dimensional im Kontext von Daten?
Dimension kennt man vielleicht als Raumdimension, man kann vor und zürck, nach links und rechts und nach oben und unten
Das sind die drei räumlichen Dimensionen
Bei Objekten sind das Länge, Höhe und Breite
Und wir fangen heute da an, wo es nur einen einzelnen Wert von einem einzelnen Objekt gibt
Wie stellt man einzelne Werte von 1-dimensionalen Größen dar?

Warum will man einzelne Werte darstellen? (00:08:19)

Warum will man einzelne Werte darstellen?
Man könnte ihn auf einen Zettel schreiben und gut ist, was gibt es da für besonderes Tricks?
Antwort: Weil man ihn wissen will
Man kann ihn auf einen Zettel schreiben, heute ist es aber oft eine digitale Anzeige
Eine einzelne Zahl auf einem Display anzuzeigen ist eine Möglichkeit einen einzelnen Wert darzustellen
Das geht in der digitalen Welt sehr leicht, aber es gibt auch heutzutage noch Gründe es anders zu machen
Um eine Zahl anzuzeigen müsste man auch digital Messen, aber es gibt noch sehr viele analoge Messgeräte
Beispiel Wasserspiegelfolge: Es gibt manchmal in Städten Orte an denen Hochwasser gezeigt werden
Manchmal ist da eine Skala und daneben Steht: hier war in dem Jahr das Hochwasser
Skala: Vertikale Linie auf der horizontale kleine Markierungen sind in regelmäßigen Abständen als Skala
Daneben stehen dann an verschiedenen Stellen Jahreszahlen, um anzuzeigen, wo das Hochwasser bereits wann stand
Das wäre eine analoge Darstellungsform für solche Daten
Der Wasserstand ist hierbei der 1-dimensionale Wert, der dargestellt wird
Nachfrage: Aber es könnte auch über eine X- und Y-Achse mit Wasserstand und Datum dargestellt werden und wäre dann nicht mehr 1-dimensional?
Genau, da würde man die Dimension der Zeit hinzunehmen
Vorteil der 1-dimensionalen Skala: Ich kann daneben stehen und habe ein Gefühl dafür, wie hoch das Wasser wirklich stand
Das erlaubt ein ganz anderes Verständnis

Welche alltäglichen Beispiele gibt es? (00:12:52)

Alltagsbeispiel Wasserkocher: hat eine analoge Skala die zeigt wie viel Wasser drin ist
Alltagsbeispiel Küchenwaage: Digitale Küchenwaage hat eine gewisse Präzision, während die analoge Küchenwaage etwas ungeneuer ist
Unterschied: Auf der digitalen können kleine Mengen besser abgemessen werden, auf der analogen große Mengen besser
Und: ich sehe bei der analogen Waage sofort, wenn ich außerhalb des Messbereiches lande, weil da ist die Skala einfach zuende
Die digitale sagt irgendwann einfach Error, wenn man die zwischendurch öfter mal nullt
Die Art der Darstellung kann daher auch von dem abhängen, was ich damit machen möchte
Alltagsbeispiel Coronaschnelltest: auch Analog, der Streifen für positiv erscheint, wenn auch mal blass, oder er erscheint nicht
Es gibt dabei also eigentlich nur zwei Zustände
Es ist auch hier klar, dass die Präzision deutlich geringer ist als ein PCR Test, aber dafür hält sich der Aufwand auch in Grenzen
Alltagsbeispiel Luftpumpe fürs Fahrrad: hat auch eine Skala für den Luftdruck
Skala ist rund, und es gibt einen Zeiger der zeigt wo gerade der Luftdruck ist
Was die Skala aber auch hat, sind weitere Markierungen die für verschiedene Reifentypen anzeigen wo der Luftdruck liegen sollte
Dadurch habe ich ein ziemlich gutes Gefühl dafür, wieviel ich noch aufpumpen muss, ohne mir konkrete Zahlen merken zu müssen
Und der eigentliche Wert ist egal, weil es um den Bereich geht
Es steht im Vordergrund schnell zu sehen, was Sache ist
Das sind jetzt viele Beispiele, bei denen es vor allem auch optische Hinweise gibt
Manchmal, wie bei dem Schnelltest, sogar ganz ohne Zahlen

Welche Vor- und Nachteile haben einzelne Zahlen? (00:17:29)

Manchmal will man die konkrete Zahl wissen und da eignet sich eben die digitale Anzeige
Vorteil: man sieht den konkreten Wert und muss nicht raten wo genau jetzt die Linie ist
Bei analogen Skalen wie einem Thermometer kann der Wert vom Blickwinkel abhängen beim Ablesen
Dadurch öhere präzision beim Ablesen
Es können auch mehrere Nachkommastellen und eine bessere Auflösung der Werte erreicht werden
Nachteil: der Wert kann genauer erscheinen als er ist (zuviele Nachkommastellen)
Kein Gefühl für Abstände zu Werten mit bestimmter Bedeutung
Das intuitive Verständnis könnte hier fehlen
Genauigkeit eines Wertes kann schlechter sein als die Auflösung, warum aber dann so viele Nachkommastellen?
Die Anzahl der Nachkommastellen nennt man Auflösung
Genauigkeit sagt, wie genau der absolute Wert ist, der da steht
Wir hatten es ja in der Temperaturdatenfolge schonmal, dass gut gesagt werden kann, wie viel Erwärmung es auf der Erde gab
Aber der Durchschnittswert der Temperatur auf der Erde nur schwer zu berechnen ist (sind es 13,5 oder 14,5 Grad?)
Heißt: Genauigkeit kann schlecht sein, aber höhere Auflösung kann trotzdem anzeigen, dass es mehr wird
Je nach Anwendung ist es also entweder sinnvoll einzelne konkrete Werte darzustellen oder eine Spannbreite in der man landet

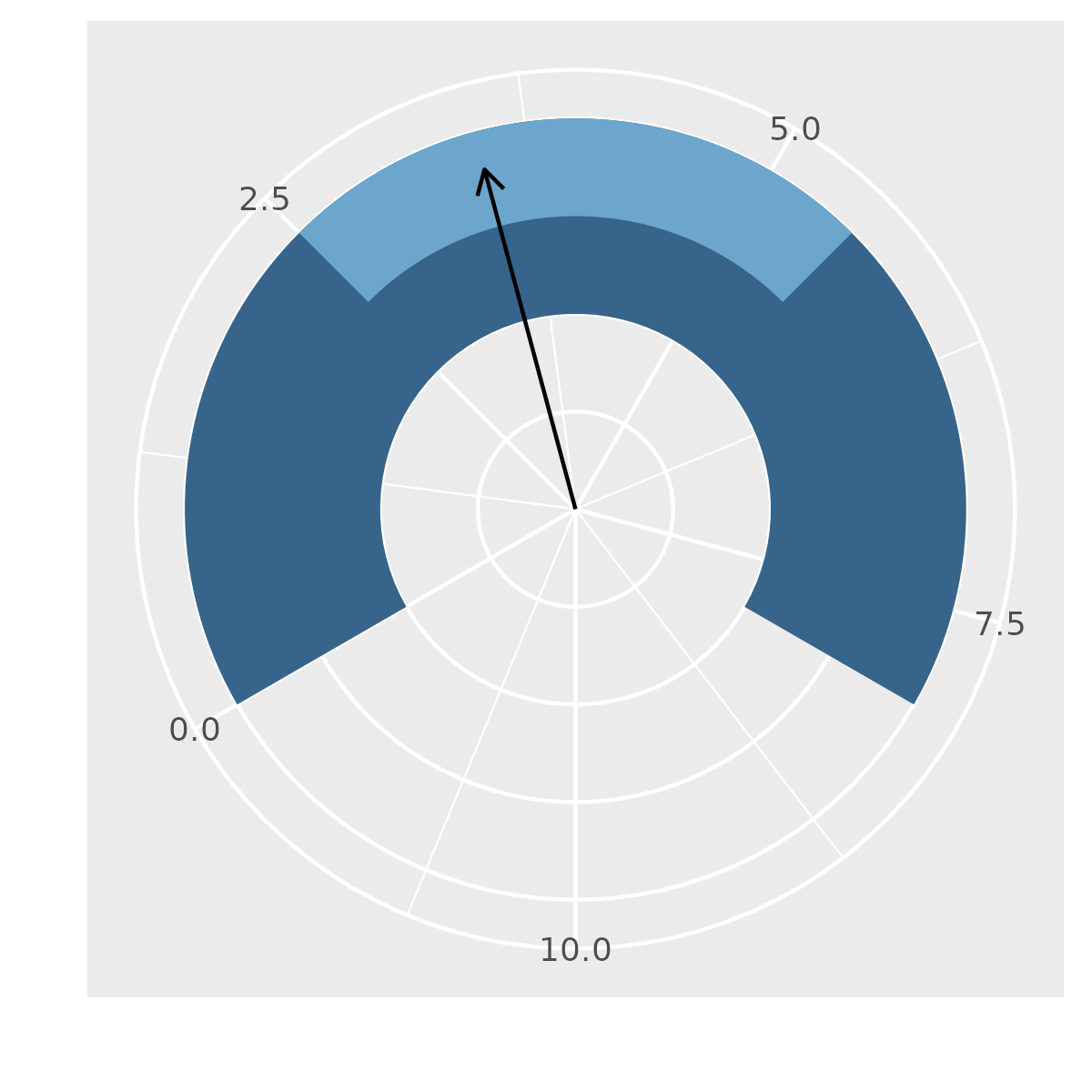
Was ist das Zeigerdiagramm (Gauge Chart)? (00:21:03)

library(ggplot2)

zeigerData <- data.frame(
  bar = "",
  druchbereich=8,
  druckmin=2.5,
  druckmax=5.5
)

p <- ggplot(zeigerData)
p <- p + geom_rect(aes(xmin = 1, xmax = 2, ymin = 0, ymax = druchbereich), fill="steelblue4")
p <- p + geom_rect(aes(xmin = 1.5, xmax = 2, ymin = druckmin, ymax = druckmax), fill="skyblue3")
p <- p + coord_polar(theta = "y", start = pi) + ylim(-2,10) + xlim(0,2)
p <- p + geom_path(
  data=data.frame(x=c(0,1.8),y=c(3.5,3.5)),
  aes(x,y),
  arrow = arrow(length=unit(0.1,"inches"))
  )
p <- p + ylab("") + xlab("") + theme(axis.text.y=element_blank(),axis.ticks.y=element_blank())
p

ggplot2::ggsave(filename="~/Projekte/podcast/029-graphentypen/zeiger.png", device="png",width=4, height = 4)

Welche guten Formen gibt es denn, etwas darzustellen, was kein absoluter Wert sein muss, sondern wo es eher eine Art Zielbereich gibt, der erreicht werden sollte?
Zeigerdiagramm: Name ist so eine Sache, englisch Gauge Chart, deutsch übersetzt als Tachometerdiagramm (von Geschwindigkeitsmessung)
Das Wort Zeigerdiagramm trifft es aber sehr genau, wenn man das Tachometer ins digitale holt
Der Begriff Zeigerdiagramm kommt aber auch in der Elektrotechnik vor im Bereich Phasendiagramm, das meinen wir hier nicht
Beispiel: Kühlwassertemperatur, fährt das Auto länger, ist der Zeiger in der Mitte bei der Normaltemperatur
Das heißt wenn der leicht nach rechts geneigt ist dass man aufpassen sollte
Landet die Temperatur oberhalb des markierten zulässigen Bereiches, am besten sofort anhalten
Wird es kritisch, gibt das Auto aber auch noch andere Signale, dass man stoppen muss
Beispiel: Tankanzeige hat einen separat hervorgehobenen Bereich, der anzeigt, dass man langsam mal tanken sollte
Zusätzlich noch eine Signallampe (die nicht teil des Diagramms sein muss), die anzeigt wenn man aufpassen sollte dass auch wirklich noch Tankstellen in der Nähe sind
Hier ist eine exakte Anzeige wie viele Liter noch im Tank sind, nicht nötig, der Bereich ist wichtig
Einige Autos berechnen auch im Boardcomputer wie viele Kilometer die Reichweite noch ist, abhängig von den Fahrtinformationen der letzten X Kilometer
Das kann auch digital angezeigt werden
Diese Beispiele sollen zeigen, dass ein Zeigerdiagramm für einen konkreten Messwert immer dann gut ist, wenn einzelne Werte eine bestimmte Bedeutung haben
Also wenn man aufpassen sollte um nicht aus einem Wertebereich rauszufallen geben einem Zeiger auch gutes Gefühl dafür wieviel Abstand man noch hat
Sie sind auch intuitiver als Zahlen
Eigentlich geht es darum Informationen zu bekommen, aber Zahlen ohne Kontext sind keine Informationen
Ein Zeigerdiagramm gibt den nötigen Kontext
Es ist besser ist, etwas sehen zu können und darüber direkt ein gut oder schlecht oder auch ein richtig oder falsch zu erkennen
Statt Zahlen ablesen zu müssen, kann der Bereich eingeschätzt werden in dem sich das befindet
Wenn man nicht sehen könnte, ob der Zeiger den richtigen Bereich verlässt oder nicht, müsste zusätzliches Wissen bestehen über die konkrete Zahl und ihre Bedeutung
Und nicht jede Person muss alles wissen, um Dinge benutzen zu können
Solche Darstellungen können etwas für mehr Menschen intuitiv benutzbar machen

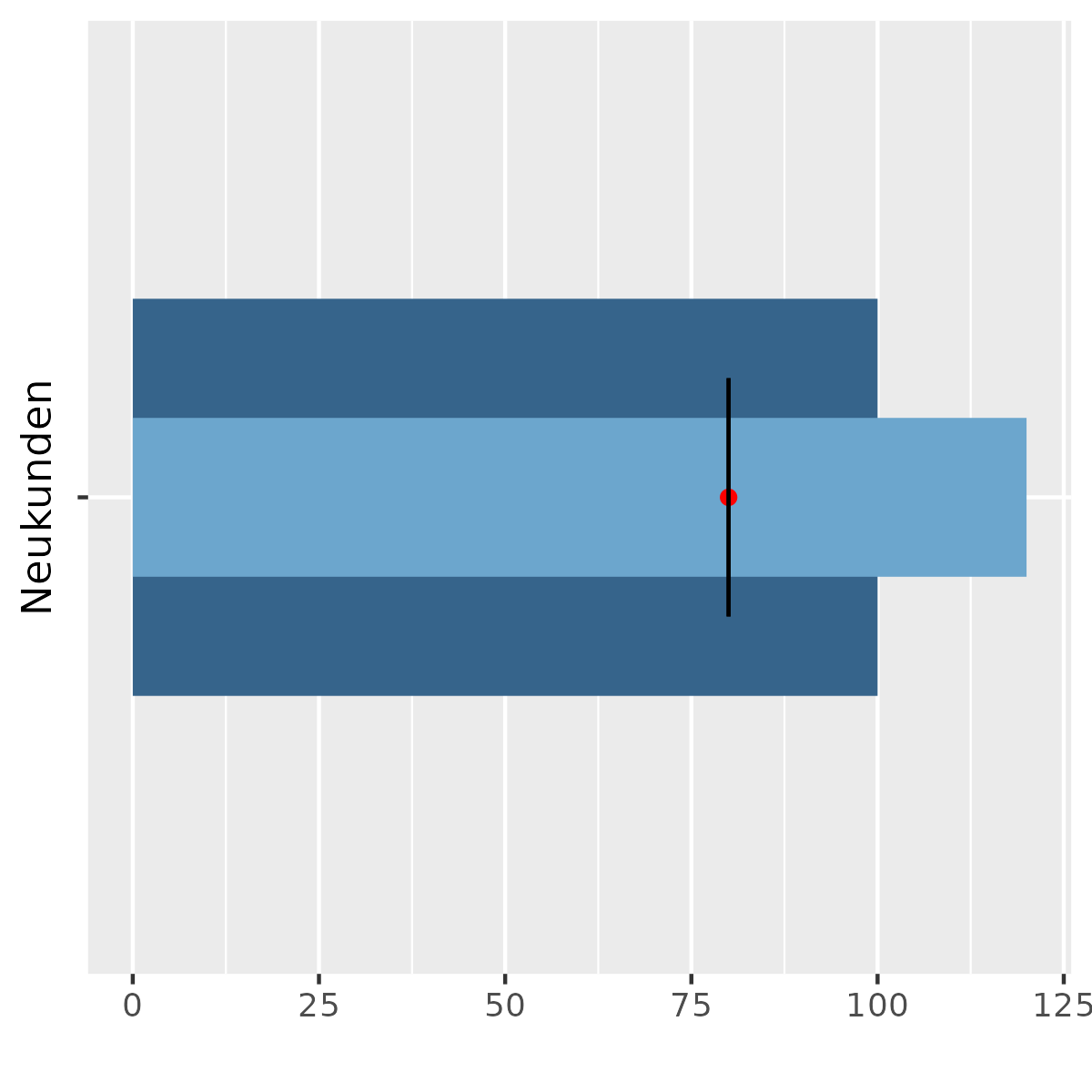
Was ist das Bullet-Chart? (00:27:18)

library(ggplot2)

bulletData <- data.frame(
  bar = "",
  Neukunden=120,
  lastyear=100,
  breakeven=80
)

p <- ggplot(bulletData)
p <- p + geom_col(aes(bar, lastyear), fill="steelblue4", width=0.5)
p <- p + geom_col(aes(bar, Neukunden), fill="skyblue3", width=0.2)
p <- p + geom_point(aes(bar, breakeven), colour="red")
p <- p + geom_errorbar(aes(y = breakeven,x = bar, ymin = breakeven,ymax
                           = breakeven), width = .3)
p <- p + coord_flip()
p <- p + ylab("") + xlab("Neukunden")
p

ggplot2::ggsave(filename="~/Projekte/podcast/029-graphentypen/bullet_chart.png", device="png",width=4, height = 4)

Ein Bullet-chart ist eine vereinfachte Fassung eines Zeigerdiagramms
Bullet ist das englische Wort für Gewehrkugel, und es geht darum, dass diese so ähnlich aussehen würden wie diese Art von Diagramm
Im Grunde nimmt man statt eines Zeigers einen Balken der den aktuellen Wert anzeigt, und färbt um den Balken herum die Bereiche gemäß ihrer Bedeutung ein
Manchmal gibt es dann noch eine Linie an der 'Zielgröße'
Ist man darüber, ist es dann gut, zum Beispiel
Bullet Chart ist immer dann gut, wenn es um Werte geht, bei denen mehr oder weniger ist besser
In den Shownotes sind auch Beispiele für ein Zeigerdiagramm und ein Bullet Chart zu sehen
Praktisches Beispiel Würfeln: Beim Rollenspiel geht es auch darum Zielbereiche/-größen mit Würfeln zu erreichen
Beim Rollenspiel werden Würfel an bestimmten stellen der gemeinsamen Erzählung eingesetzt, um zu gucken, was passiert
Beispiel: Ein Charakter klettert einen Baum hoch und es wird gewürfelt ob und wenn wie gut es gelingt
Es werden 2 sechsseitige Würfel geworfen, gelungen ist die Probe, wenn nur einer der beiden Würfel eine 5 oder eine 6 anzeigt
Das ist also der Zielbereich, den es zu erreichen gilt
Bei einer 1-3 hat man es nicht geschafft
Bei einer 4 könnte man es schaffen, wenn man vorher sagt, dass man sich Zeit nimmt und konzentriert
Je höher der Wurf, desto besser, aber es gibt auch einen Zwischenbereich, der manchmal gut ist
Mindestens für das deutsche Tiny Dungeon gibt es Würfel, die ausserdem farblich markiert sind
Die Zahlen 1-3 auf den Würfeln sind rot, 4 ist orange und 5-6 sind grün
Und das klingt dann schon sehr nach dem Bullet Chart und je größer die Zahl, desto besser passt auch
Aber brauche ich dann überhaupt Zahlen, reichen nicht die Farben?
Wenn es eine vergleichende Probe ist, können auch die konkreten Zahlen wichtig werden
Wichtig ist aber: allein an der Farbe kann ich schon erkennen, ob ich den Zielbereich getroffen habe
Es ist intuitiv erkennbar und das ablesen der Zahlen ist nicht nötig
Beispiel Neukundenaquise: Eine Firme möchte die Anzahl an Neukunden betrachten
Farblich hinterlegt sind dann zum Beispiel break-even points, also ab wo keine Verluste mehr entstehen
Dann vielleicht auch der Vorjahreswert als Linie und auch das aktuelle Ziel und der Balken zeigt den aktuellen Wert an
Auch hier ist nicht mehr relevant wie die Zahl ist, sondern die Relation zu den anderen Informationen
Ist also eine Unterscheidung zu treffen zwischen dem 1-dimensionalen Datenpunkt und in der Darstellung dann den Kontexten dazu?
Ja, man kann den aktuellen Wert sehr gut ablesen, aber der Kontext kann auch sehr gut vermittelt werden
Das, was um den Wert herum ist, spielt eine Rolle
Der 1-dimensionale Wert bleibt 1-dimensional, aber durch den Kontext wird aus ihm Information

Fazit (00:37:47)

1-dimensionale Daten sind Datenpunkte, die mit einem einzigen Wert beschreibbar sind
Informationen und Daten sind nicht das Gleiche
Und eine Zahl allein sagt nicht viel, man muss den Kontext wissen
Zeigerdiagramme sind zum Beispiel eine Möglichkeit, um Kontext zu liefen
Und es ist von Vorteil, wenn Werte intiutiv lesbar sind und ersichtlich ist, was ausgedrückt werden soll, auch ohne zusätzliches Wissen
Die Darstellung und für welche man sich entscheidet, ist auch immer kontextabhängig

Nächste Folge: offene Daten im Oktober (00:39:48)

Wir reden mal wieder über offene Daten, aber dieses mal im Allgemeinen
Wofür braucht man das, was kann man damit tun?
Wir werden ein paar Beispiele anführen, wo offene Daten vorkommen und zu finden sind
Und uns vor allem mit den Bereichen forschung und politik befassen

Call to Action (00:40:25)

Wenn ihr uns weiter hören möchtet, folgt uns auf Twitter unter @datenleben & Mastodon unter @datenleben@chaos.social
Oder besucht unsere Webseite: www.datenleben.de
Hinterlasst uns gerne Feedback, wir würden uns darüber sehr freuen
Ihr könnt uns als Data Scientists auch Buchen für Analysen oder Projekte
Habt ihr Fragen oder Themen, die euch interessieren? Dann schreibt uns!

Outro (00:41:24)

Schlagworte zur Folge

Datenpunkt, Datenpunkte, 1-dimensionale Daten, Graphen, Bullet Chart, Zeigerdiagramm, Gauge Chart